Nierównośc z wartościami bezwzglednymi Kick: |x|+|y|<=1 mógłby ktoś pomógł rozwiązac?

ICSP: rozpisz na 4 przypadki.

Kick: x+y<=1 x−y<=1 −x−y<=1 −x+y<=1 takie?

ICSP: 1^o x > 0 oraz y > 0 2^o x > 0 oraz y < 0 3^o x < 0 oraz y > 0 4^o x < 0 oraz y < 0

pigor: ....analitycznie (rachunkowo) to np. tak : |x|+|y| ≤ 1 ⇔ [xy< 0 i (−x+y ≤ 1 lub x−y ≤ 1)] lub [xy ≥0 i (x+y ≤ 1 lub −x−y ≤ 1)] ⇔ ⇔ [xy< 0 i (y ≤ x+1 lub y ≥x−1)] lub [xy ≥0 i (y ≤ −x+1 lub y ≥−x−1)] , co graficznie oznacza to zbiór punktów (x,y)∊R² − płaszczyzny z układem xOy w II i III ćw. (y ≤ x+1 lub y ≥ x−1) lub w I i IV ćw. (y ≤ −x+1 lub y ≥ −x−1) . ...

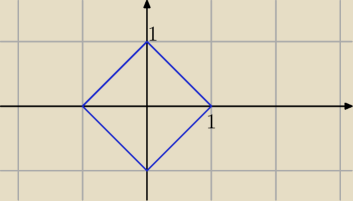
vitek1980: rozwiązaniem jest zbiór punktów (x,y) należących do kwadratu o wierzchołkach (0,1) (1,0) (0,−1) (−1,0)

pigor: ..., a może dla niektórych, którzy za kwadrat biorą to co widzą na niebiesko , powiem odp. nieco inaczej: rozwiązaniem danej nierówności jest zbiór punktów (x,y) wnętrza kwadratu i jego brzegu.