.
E:
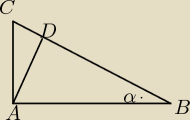
W trójkącie prostokątnym ABC poprowadzono wysokość AD na przeciwprostokątną BC. Jeśli CD=1 i
DB=4, to tangens kąta ostrego α wynosi
kompletnie nie mam pojęcia jak to zrobić, niech mi to ktoś wytłumaczy, proszę :C
ICSP: Jest taki wzór (dla tójkąta prostokątnego i dla danych podanych na tym rysunku)
|AD|
2 = |CD| * |BD| − z tego policzysz |AD|
| | AD | |
później wystarczy zauważyć ze z definicji tangensa masz od razu : tgα = |
| |
| | DB | |
5-latek : Ten wzor co podal
ICSP wynika z takiego twierdzenia . W trojkacie prostokatnym wysokosc
opuszczona z wierzcholka kata prostego na przeciwprostokatna dzieli ja na dwie czesci w taki
sposob ze jest dla tych czesci srednia geometryczna . My oczywiscie wiemy ze srednia
gepmetryczna np 2 liczb x i y to
√x*y a 3 liczb x,y z to
√x*y*z itd
Czyli u nas wysokosc to bedzie |AD| a czesci na jakie podzielila ta wysokosc
przeciwprostokatna |CB| to |CD i BD| to zgodnie z tym twierdzeniem mozemy zapisac ze
|AD|=
√|CD|*BD|
Jesli teraz obie strony tego ostatniego rownania czyli
|AD|=√|CD|*|BD| podniesiemy do
kwadratu z eby pozbyc sie pierwiastka to otrzymamy wzor ktory podal
ICSP
czyli
|AD2|=|CD*BD|
dane masz wiec sobie podstaw i licz . Oczywiscie w tym przypadku to rownanie AD=
√CD*BD nie
musisz podnosic do
2 bo to wyjdzie ladny pierwiastek .
