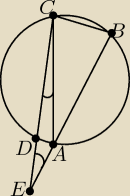
Długości cięciw, miary kątów. belzebubek: Długości cięciw AB, BC i CD sa równe, |∠E| = 20°. a) Oblicz miarę kata ACD. b) Oblicz długość odcinka AC, jeśli |CE| = 6. Wynik zaokrąglij do części dziesiątych.

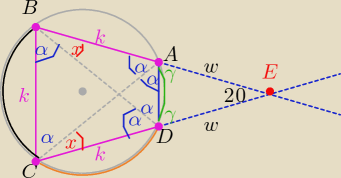Eta: 1/ Trójkąty równoramienne : ABC, BCD i przystające trójkąt ADE równoramienny o kącie między ramionami 20^o ( z treści zad) 2/ Zauważ kąty wpisane oparte na tych samych łukach 3/ z warunku wpisania czworokąta ABCD w okrąg: α+x+2α=180^o ⇒ (*) 3α+x= 180^o 4/ w trójkąt BCE (równoramiennym) α+x+α+x+20^o=180^o ⇒ (**) α+x= 80^o rozwiązując układ równań: (*) i (**) otrzymasz : |∡ ACD|=x= 30^o i α=50^o b) w trójkącie ACE z tw. sinusów wiedząc,że γ= 180^o−2α= 80^o.to |∡CAE|= 130^o |CE|= 6 i sin130^o= sin 50^o

	|CE|		|AC|
		=
	sin130o		sin20o

	6*sin20o
|AC|=		= ......... sin20o =.... , sin50o=... odczytaj z tablic
	sin50o

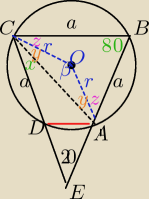Mila: W ΔBCE: ∡C=∡B=(180−20):2=80β ∡β=2*80=160 jako środkowy oparty na tym samym łuku co wpisany∡B=80⁰ ∡y=(180−160):2=10⁰ ∡z=(360−80−200):2=40 ∡x=80−(z+y)=80−(40+10)=30⁰

Eta:

belzebubek: kurcze, przecież to było całkiem proste x.x dzięki za pomoc

Mila: