zadania aza: Zadania dla bezendu i Saizou ( coby się nie nudzili 1/ Wykaż ,że jeżeli a>2 i b<4 to b+2a >U{ab}{2+4 2/ wykaż,że jeżeli x>m , to wyrażenie: W= x³+5x−mx²−5m przyjmuje tylko wartości dodatnie w zbiorze R 3/ Wykaż,że jedynym rozwiązaniem równania: x²+y²−12x+2y+37=0 jest para liczb (6, −1) 4/ wykaż ,że w pięciokącie foremnym o boku a długość przekątnej d jest równa:

	a
d=		(√5+1)
	2

5/ W trójkącie prostokątnym ABC z punktu P należącego do przeciwprostokątnej BC poprowadzono odcinki PD i PE prostopadłe odpowiednio do przyprostokątnych AC i AB Wykaż,że

	|PD|		|PE|
		+		=1
	|AB|		|AC|

aza: Poprawiam zad 1/

	ab
Wykaż,że b+2a>		+4
	2

Saizou : Eto jak ty o nas dbasz 1) Zał : a>2 i b<4

	ab
Teza: b+2a>		i pytanie czy w mianowniku ma być 2+4 ?
	2+4

Ajtek: Witaj Eta . Ciekawe zdanka, 3 zrobiłem w pamięci .

Ajtek: Cześć Saizou .

bezendu: Saizou zadanie 3 nie tykać

Saizou : a 3 jest fajne

Ajtek: Cześć bezendu .

bezendu: x²+y²−12x+2y+37=0 x²−12x +36−36 +y²+2y +1−1 +37=0 (x−6)² −36 + (y+1)² −1 +37=0 (x−6)²+(y+1)²=0 x=6 y=−1 C.N.D

bezendu: Witaj Ajtek

aza: Mogę Wam napisać jeszcze więcej ...... zadań, oczywiście

Godzio: Uzupełnienie do 4 dla ciekawskich:

	d
Czym jest stosunek		?
	a

aza: @ bezendu ( co to za punkt?

Vizer: bezendu brakuje uargumentowania jeszcze dlaczego tylko te rozwiązania spełniają to równanie

aza: złotko.... Godzio

Ajtek: Cześć Godzio .

bezendu: zadanie 3 promień wynosi 0 a równanie okręgu (6,−1) czyli okrąg nie ma promienia tylko środek teraz może być ?

Godzio: Cześć Eta, kiedyś dałaś mi w nieco innej formie to zadanie

bezendu: Czy teraz zadanie 3 się zgada ? bo nie wiem czy brać się za następne czy to poprawiać ?

Saizou : ten środek to po prostu punkt

aza: 6/ W trapezie o podstawach a>b , suma miar kątów ostrych jest równa 90^o . Wykaż,że odcinek łączący środki podstaw trapezu ma długość

	a−b
	2

Vizer: Nie jest to równanie okręgu, bo promień musi być dodatni, co to za okrąg o promieniu 0

aza: To równanie nie przedstawia okręgu , tylko punkt S

Vizer: Odpowiednim wyjaśnieniem na to jest to, że jest to suma kwadratów dwóch jakichś liczb, które by były równe zero, to każda z nich musi być równa 0

Eta:

bezendu:

ab
	+4<b+2a /2
2

ab+8<2b+4a ab−2b<4a−8 b(a−2)<4(a−2) b(a−2)−4(a−2)<0 (a−2)(b−4)<0 C.N.D

Vizer: Przepraszam Eta za napisanie rozwiązania, już nie będę

pigor: .., nie musisz nic wiedzieć o równaniu okręgu, wystarczy tylko znajomość wzorów skróconego mnożenia , bo np. tak : x²+y²−12x+2y+37=0 ⇔ x²−12x+36+y²+2y+1=0 ⇔ (x−6)²+(y+1)²=0 ⇔ ⇔ x−6=0 i y+1=0 ⇔ x=6 i y=−1 ⇔ (x,y)=(6,−1) . ...

Vizer: Zawsze mnie zastanawiało to dlaczego pigor zawsze pisze wielokropek na początku i na końcu swojej wypowiedzi To chyba tylko tak z nawyku jakiegoś, nie?

Eta: Zadanie dla pigora ( bo się "pali" do rozwiazań Oblicz dokładną wartość cos36^o =.......

Vizer: I sobie nagrabił u Ety Dobrze, że ja przeprosiłem

Eta: ......"no to tak".......i jeszcze dodaje

Ajtek: Witaj pigor . Wg mnie zapis pigora, czyli na początku ... i na końcu, odpowiada zapisowi odpowiednio: na początku (...) i na końcu (...) wtrącenie swojego zdania do problemu.

bezendu: zadanie 1 czeka do sprawdzenia

Eta: w zad1/ brak w zakończeniu komentarza !

Vizer: bezendu nic nie udowodniłeś

Saizou : to ja się wezmę za zadanie 2 choć będzie ciężko bo dzisiaj 30 km na rowerku

Eta: "tyz prowda".........

bezendu: zaraz dopiszę jakiś komentarz stosowny

Eta: No

Ajtek: Saizou przecież nie pedałowałeś głową, tylko nogami . Nogi do matmy nie są potrzebne, sama głowa i sprawna ręka wystarczą .

pigor: jak już tak się zapaliłaś, to rozwiąż sobie Eta np. równanie : cos 36^o= sin54^o2 ⇔ cos2α= sin3α , gdzie α=18^o, bo mnie się nie chce. ...

bezendu: a>2 i b<4 a−2>0 b−4<0 więc teraz ta nierówność na pewno zachodzi

Eta: dla pigora Zanim zjesz, to ........... młodzi rozwiążą zadania .... sami

bezendu: Zadanie 6 <pyta się> ten trapez nie może być prostokątny ?

Saizou : zad. 2 W= x³+5x−mx²−5m x³−mx²+5x−5m= x²(x−m)+5(x−m)= (x²+5)(x−m) x²+5 zawsze przyjmuje wartości dodatnie x−m , gdy x>m też przyjmuje wartości dodatnie zatem ich iloczyn przyjmuje tylko wartości dodatnie

Vizer: Już dobrze, ale można było też podzielić przez (a − 2), wiedząc że jest to wyrażenie dodatnie i doszedłbyś do b < 4 co jest prawdą dla naszego założenia.

bezendu: Saizou żebym nie był samolubny zostawiam Ci zadanie 4,5

Saizou : 4 zadanko jest prosto z tw. cosinusów zrobić

Eta: @[bezendu]] ......... nie osłabiaj mnie....... tym trapezem prostokątnym ?

bezendu: dobra już wiem chyba jak zrobić to zadanie 6

Eta: @ Saizou proste? .......... to podaj rozwiązanie

pigor: ..., (ten początek i koniec − tak − to mój ślad) a co do zadania 1 − i już znikam,aby się nie zapalić − np. tak : a>2 i b<4 ⇔ a−2>0 i 4−b>0 ⇒ (a−2)(4−b) >0 ⇔ 4a−ab−8+2b >0 /:2 ⇔ ⇔ 2a−¹₂ab−4+b >0 ⇔ b+2a > ¹₂ab+4 c.n.w. . ...

Eta: i

Saizou : właśnie sobie uświadomiłem że cos108 nie jest tak proso obliczyć

Eta: Acha? .........

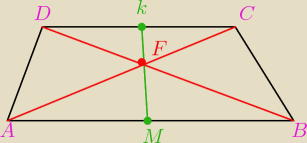
bezendu: odcinek |AB| to podstawa a odcinek |CD| to podstawa b zgodnie z założenia a>b K to punkt środka odcinka |DC| a punkt M to środek odcinka |AB| F środek odcinków |DB| i |AC| zaraz dopisze resztę jak to do tej pory jest ok ?

Eta: Działaj dalej i zaznacz kąty ostre !( może Ci się rozjaśni ?

pigor: ..., skorzystaj np. z mojego postu z godz. 22⁰⁴ i tego, że cos108^o= cos(90^o+18^o)= −sin18^o . ...

Eta: Echh pigor

Saizou : Eta nie masz po co kiwać, bo wzory redukcyjne od razu zastosowałem

Ajtek: Cos kiedyś Godzio mnie podpuścił z dowodem na cos36^o chyba. Poszukaj na forum , jakiś rok temu mniej więcej.

Eta: Następny litościwy ........

Ajtek: Eta, że ja

JAPON1A: cos 36 przez trojkat równoramienny sie liczy, tak ?

Eta: A kto? ...... jasne,że Ty

Eta: @Japonka .... też tak można

Ajtek: Eta, łapka wysunięta do dostania liniałem gotowa .

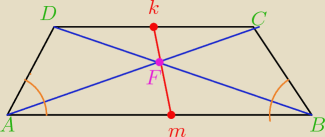
bezendu: α+β=90

|AM|		|AF|		1
	=		=
AB		|AC|		2

z tego mam że odcinek środka |KM| jest równoległy do |BC| ale dalej nie wiem jak ?

bezendu: nie środek tylko odcinek KM jest równoległy do odcinak CB

bezendu: Dobra ja już dziś odpuszczam ale mam taką prośbę gównie do Saizou nie wstawiaj swojego rozwiązani do zadania 4, 5 i 6 poczekaj do jutra i jak @Eta możesz to daj jeszcze jakieś zadanka, żeby jutro można było po południu zrobić Dziękuje za uwagę i dobranoc

Ajtek: Spokojnej nocki Bezendu . Taż cos wrzucę, jak znajdę zbiorek

Eta: Na razie odpocznij ( jutro coś wrzucę Dobranoc

bezendu: Jeszcze jurto wrzucę po południu zadanka z matury roz oczywiście do sprawdzenia czy dobrze zrobiłem

Eta: ok

Saizou : wpadłem na pomysł jak robić zadanie o pięciokącie bez wyliczania funkcji trygonometrycznych

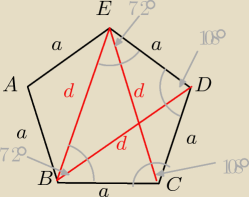
Saizou : zauważam że na czworokącie BCDE można opisać okrąg, zatem z tw. Ptolemeusza otrzymam a²+ad=d² d>a>0 a²+ad−d²=0 /a²

	d		d		d
−(		)2+		+1=0		=t t>0
	a		a		a

−t²+t+1=0 Δ=1+4=5 √Δ=√5

	−1−√5		√5+1
t1=		=
	−2		2

	−1+√5
t2=		sprzeczność bo t2<0
	−2

√5+1		d
	=
2		a

	√5+1
d=		a
	2

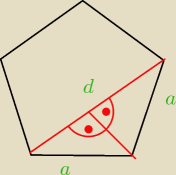
bezendu: (5−2)*180=3*180=540:5=108 d²=a²+a²−2*a*acos108 a²+a²+2a²cos(180−72) a²+a²+2a²cos72^o 2a²+2a²cos72^o 2a²(1+0,3090) d²=2,618a² d=a√2,618=1,618

	a
d=		(√5+1})
	2

C.N.D

Saizou : a czemu używałeś wartości przybliżonej? wypadało by podać dokładną wartość dlatego ja zrezygnowałem z tw. cosinusów

bezendu: wartość dokładną jak chcesz to możesz się pobawić w wartość dokładną masz zadanie 5 ?

Saizou : nie ale wyczuwam podobieństwo trójkątów

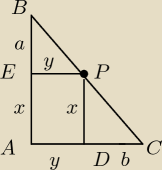
Saizou : ΔCDP~ΔBEP

a		x
	=
y		b

ab=xy / obustronnie dodaję bx+ya+xy bx+xy+ya+xy=ab+ya+bx+xy x(b+y)+y(a+x)=a(b+y)+x(b+y)

	1
x(b+y)+y(a+x)=(b+y)(a+x) /*
	(a+x)(b+y)

x(b+y)+y(a+x)
	=1
(a+x)(b+y)

x		y
	+		=1
a+x		b+y

PD		PE
	+		=1
AB		AC

cnu

Eta: 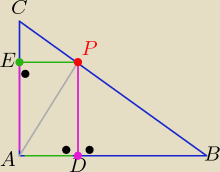2 sposób

	1		1
P(APC) =		|AC|*|PE| i P(ABP)=		|AB|*|PD|
	2		2

	1
P(ABC)=		|AB|*|AC|
	2

P(APC)+P(ABP)= P(ABC) to: |AC|*|PE|+|AB|*|PD| = |AB|*|AC| /: |AB|*|AC| ≠0

	|PD|		|PE|
		+		= 1
	|AB|		|AC|

c.n.u

5-latek :

	1
bezendu cos 72stopni =		(√5−1)
	4

	1
sin72 stopni=		(√10+2√5)
	4

tg72stopni = √5+2√5)

	1
cos36 stopni =		(√5+1)
	4