Oblicz pole powierzchni i obwód trójkąta ABC.
wajdzik:
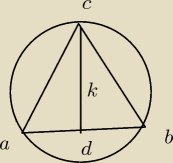
W trójkącie ABC długości boków AC i BC są równe. Okrąg, którego średnią jest wysokość CD
trójkąta ABC przecina boki trójkąta w punktach dzielących te boki w stosunku 4:1, licząc od
wierzchołka C. Oblicz pole powierzchni i obwód trójkąta ABC, mając daną długość wysokości CD
równą k.
|AC|=|BC|
(4x
2)+x
2=k
2
17x
2=k
2
| | 1 | | k√17 | | √17 | |
P= |
| *k* |
| = |
| [j2] |
| | 2 | | 17 | | 34 | |
To jest chyba źle... a co drugiej części to nie mam pojęcia.
| | a+b+c | |
Mam wyliczyć chyba połowę obwodu ze wzoru p= |
| |
| | 2 | |
ale nie mam ani b ani c, chyba, że to jest trójkąt równoboczny...?

Proszę o pomoc

30 maj 19:54
krystek: Dobrze zapisałeś treśc ?
30 maj 20:20
krystek: CD=2R ?
30 maj 20:20
wajdzik: Treść jest dobrze przepisana

30 maj 20:23
5-latek : Zastanow sie sam nad trescia jeszcze raz . Jak moze byc wysokosc trojkata na ktorym jest
opisany okrag byc jego srednica (popatrz na swoj rysunek ) . Poprowadz wysokosc do konca i
sprobuj narysowac trojkat
30 maj 20:33
pigor: ..., zły rysunek zrobiłeś ; cyrkiel włóż w środek wysokości Δ i zakreśl okrąg o promieniu
równym połowie tej wysokości i wtedy rozwiązuj zadanie . ...

30 maj 20:39
krystek:
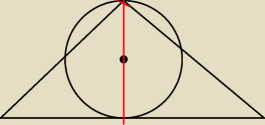
30 maj 20:45
aza:
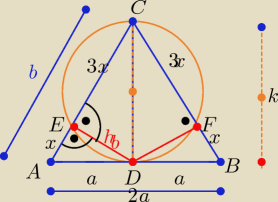
Z podobieństwa trójkątów AE i DEC
|ED|
2= 3x*x ⇒ |ED|=
√3x , x>0
to |AD|=a= 2x zatem |AB|= 4x= |AC|= |BC|
zatem trójkąt ABC jest równoboczny o boku
4x
| | k | | √3 | |
z tw. Pitagorasa : (4x)2−x2=k2 ⇒ x= |
| = |
| k |
| | √12 | | 6 | |
Ob(ABC)= 12x=.........
P(ABC)= a*k = ......
dokończ ........
30 maj 21:15
pigor: ... , czyżby

, niestety w stosunku 4:1 to znaczy 4x i x , a nie jak powyżej .
30 maj 21:32
aza:
O kurcze

jak ja patrzyłam

( ślepota)
dzięki
pigor z poprawkę

A tak pięknie rysowałam i "zdechło" !
@
wajdzik popraw i zapisz zamiast x i 3x ......... x i 4x
30 maj 21:35
pigor: ... przepraszam

, nie wiedziałem, że to Ty ..., choć po rysunku powinienem poznać

30 maj 22:20
Eta:

30 maj 22:23
wajdzik: wow, masz talent Azo

Dzięki wielkie

30 maj 23:34
Eta:

30 maj 23:35
wajdzik: Azo, tam się wkradł mały błąd jeszcze chyba: jak stosowałaś tw.Pitagorasa 16x
2−x
2=15x
2 a nie
12x
2. Dobrze to widzę prawda?

31 maj 10:09
wajdzik: 
31 maj 13:04
wajdzik: 
31 maj 13:23
Eta:
Poprawiam :
|AE|= x |EC|= 4x , x>0
|DE|
2= x*4x= 4x
2 ⇒ |DE|= 2x
z tw. Pitagorasa w trójkącie ADE
a
2=x
2+4x
2 ⇒ a=
√5x
i z tw. Pitagorasa w trójkącie ADC
| | k | | √5 | | 1 | |
25x2−5x2= k2 ⇒ x= |
| = |
| k to a= |
| k |
| | √20 | | 10 | | 2 | |
P= a*k=..........
Ob: L= 10x+ 2a=.........
31 maj 16:04
1 cze 21:41
wajdzik: P=2 [j2] zgadza się?
1 cze 21:41
wajdzik: 
1 cze 22:56
wajdzik: | | √5 | |
czegoś tu nie rozumiem, jeśli k=√20x i okazuje się, że x= |
| k to ile wynosi k? |
| | 10 | |
1 cze 23:17
1 cze 23:25
wajdzik: | | √5 | |
k=1, bo k=√20*x=√20* |
| =1 |
| | 10 | |
1 cze 23:27
1 cze 23:27
1 cze 23:28
wajdzik: Eta, jak będziesz mogła to sprawdź

1 cze 23:28
wajdzik: 
2 cze 14:17
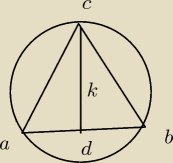 W trójkącie ABC długości boków AC i BC są równe. Okrąg, którego średnią jest wysokość CD
trójkąta ABC przecina boki trójkąta w punktach dzielących te boki w stosunku 4:1, licząc od
wierzchołka C. Oblicz pole powierzchni i obwód trójkąta ABC, mając daną długość wysokości CD
równą k.
|AC|=|BC|
(4x2)+x2=k2
17x2=k2
W trójkącie ABC długości boków AC i BC są równe. Okrąg, którego średnią jest wysokość CD
trójkąta ABC przecina boki trójkąta w punktach dzielących te boki w stosunku 4:1, licząc od
wierzchołka C. Oblicz pole powierzchni i obwód trójkąta ABC, mając daną długość wysokości CD
równą k.
|AC|=|BC|
(4x2)+x2=k2
17x2=k2
 Proszę o pomoc
Proszę o pomoc 



 Z podobieństwa trójkątów AE i DEC
|ED|2= 3x*x ⇒ |ED|= √3x , x>0
to |AD|=a= 2x zatem |AB|= 4x= |AC|= |BC|
zatem trójkąt ABC jest równoboczny o boku 4x
Z podobieństwa trójkątów AE i DEC
|ED|2= 3x*x ⇒ |ED|= √3x , x>0
to |AD|=a= 2x zatem |AB|= 4x= |AC|= |BC|
zatem trójkąt ABC jest równoboczny o boku 4x
 , niestety w stosunku 4:1 to znaczy 4x i x , a nie jak powyżej .
, niestety w stosunku 4:1 to znaczy 4x i x , a nie jak powyżej .
 jak ja patrzyłam
jak ja patrzyłam  ( ślepota)
dzięki pigor z poprawkę
( ślepota)
dzięki pigor z poprawkę A tak pięknie rysowałam i "zdechło" !
@ wajdzik popraw i zapisz zamiast x i 3x ......... x i 4x
A tak pięknie rysowałam i "zdechło" !
@ wajdzik popraw i zapisz zamiast x i 3x ......... x i 4x
 , nie wiedziałem, że to Ty ..., choć po rysunku powinienem poznać
, nie wiedziałem, że to Ty ..., choć po rysunku powinienem poznać 

 Dzięki wielkie
Dzięki wielkie 






