Funkcja homograficzna
szymon: Witam. Bardzo proszę o rozwiązania do tych zadań, bo muszę się nauczyć do poprawy, a mam nie
ciekawą sytuację z matematyki. Dobrze by było gdyby wszystkie było rozwiązane, ale będę się
cieszył nawet z jednego.
http://scr.hu/0k3o/t07n3
30 maj 15:34
aniabb:
30 maj 15:37
aniabb:
30 maj 15:39
aniabb:
30 maj 15:41
aniabb:
30 maj 15:42
aniabb:
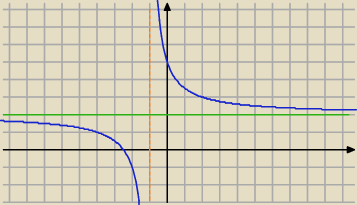
niebieskie mniejsze równe zielone
czyli x∊(−
∞;−1)
30 maj 15:45
aniabb:
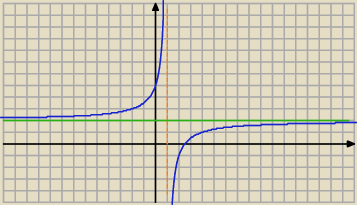
niebieskie mniejsze równe zielone
czyli x∊(1;
∞)
30 maj 15:47
aniabb:
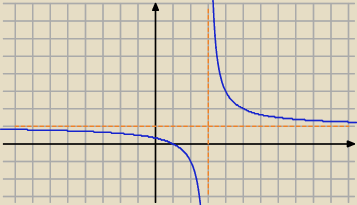
wyznaczone y
30 maj 15:50
aniabb:
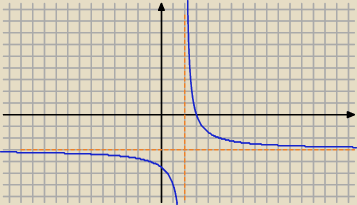
wyznaczone y
30 maj 15:51
Basia: Sądzisz Aniu, że ktoś kto musi walczyć o pozytywną ocenę będzie wiedział jak te wykresy
powstały i potrafi rozwiązać podobne zadania ?
30 maj 16:54
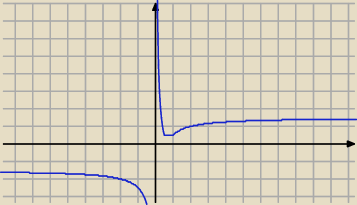
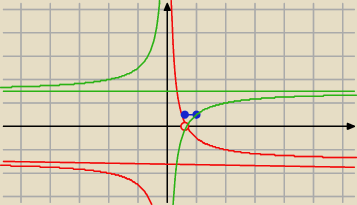
Kronos: coś mi się nie zgadza w tym pierwszym wykresie, bo w trzecim przedziale wyszła mi asymptota
pozioma 1, a ten wykres przecina tę asymptotę. Czy mam błąd w obliczeniach ?
30 maj 17:58
Basia:
o ten przykład Ci chodzi ?
30 maj 18:13
Kronos: Tak
30 maj 18:16
Basia:
x∊(−
∞,0)∪(0;
12) ⇒
| | −2x+1−x+1 | | −3x+2 | | 3 | | 1 | | 1 | | 3 | |
f(x) = |
| = |
| = − |
| + |
| = |
| − |
| |
| | 2x | | 2x | | 2 | | x | | x | | 2 | |
x∊<
12;1) ⇒
| | 2x−1−x+1 | | x | | 1 | |
f(x) = |
| = |
| = |
| |
| | 2x | | 2x | | 2 | |
x∊<1;+
∞) ⇒
| | 2x−1+x−1 | | 3x−2 | | 3 | | 1 | | 1 | | 3 | |
f(x) = |
| = |
| = |
| − |
| = − |
| + |
| |
| | 2x | | 2x | | 2 | | x | | x | | 2 | |
to czerwone tylko do
12 czyli do czerwonego kółka
potem niebieskie, potem zielone
30 maj 18:31
Mila:
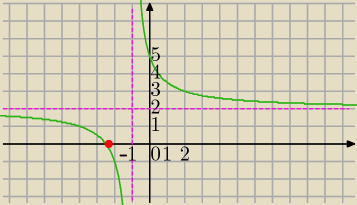
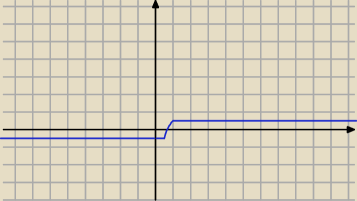
Zadanie 4)
1)Dziedzina:
x+1≠0⇔x≠−1
D=R\{−1}
x=−1 asymptota pionowa
2) Zbiór wartości:
| | 2x+5 | |
y= |
| przekształcamy do postaci kanonicznej |
| | x+1 | |
y=2 asymptota pozioma
Z
W=R\{2}
Patrz wykres
3) f(x)≤2
f(x)≠2
f(x)<2 dla x<−1
4) miejsce zerowe
2x+5=0 i x∊D
x=−2,5
30 maj 18:55
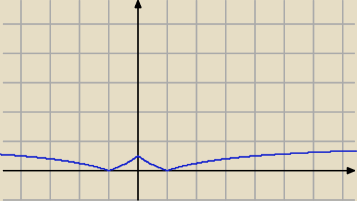
Mila:
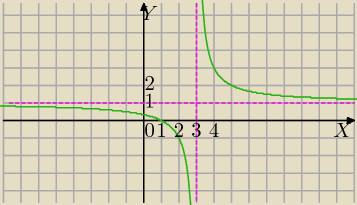
5) wyznacz y w zależności od x.
xy−x−3y+1=0
xy−3y=x−1
y(x−3)=x−1
D=R\{3}
przekształcenie do postaci kanonicznej
x=3 asymptota pionowa
y=1 asymptota pozioma
Wykres
30 maj 19:03
30 maj 19:36
Mila:
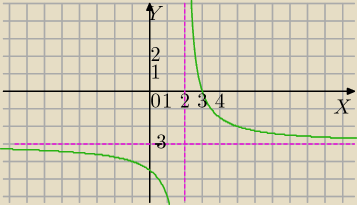
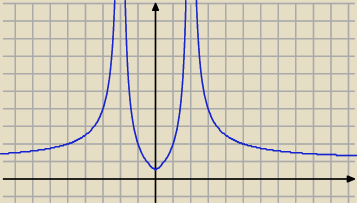
6)
WYZNACZ Y Z RÓWNANIA w zależności od x.
xy+3x−2y−9=0
xy−2y=−3x+9
y(x−2)=−3x+9
D=R\{2}
| | −3x+9 | |
y= |
| przekształcenie do postaci kanonicznej: |
| | x−2 | |
x=2 asymptota pionowa
y=−3 asymptota pozioma
Z
w=R\{−3}
30 maj 20:01






 wyznaczone y
wyznaczone y
 wyznaczone y
wyznaczone y
 x∊(−∞,0)∪(0;12) ⇒
x∊(−∞,0)∪(0;12) ⇒
 Zadanie 4)
Zadanie 4)
 5) wyznacz y w zależności od x.
xy−x−3y+1=0
xy−3y=x−1
y(x−3)=x−1
5) wyznacz y w zależności od x.
xy−x−3y+1=0
xy−3y=x−1
y(x−3)=x−1
 6)
WYZNACZ Y Z RÓWNANIA w zależności od x.
xy+3x−2y−9=0
xy−2y=−3x+9
y(x−2)=−3x+9
6)
WYZNACZ Y Z RÓWNANIA w zależności od x.
xy+3x−2y−9=0
xy−2y=−3x+9
y(x−2)=−3x+9