zbieżność ewelina: mógłby ktoś opisac zbieżność funkcji. y=e^x * cosx , y=e^x * sinx y=lnx + 4x⁶ wiem że to długie zadanie, ale nie rozumiem go. Zrobcie 1 jako przykład, resztę sama spróbuje zrobić i pokaże co mi wyszło

ewelina: *zbadać nie opisać

Artur_z_miasta_Neptuna: sprawdź treść zadania ... nie ma czegoś takiego jak badanie zbieżności funkcji

ewelina: źle napisałam : muszę zbadać przebieg zmienności funkcji.

Basia: f(x) = e^x*cosx 1. dziedzina x∊R 2. ponieważ nie ma punktów nieciągłości badasz granicę przy x→±∞ granica przy x→+∞ n ie istnieje dlaczego ? weźmy ciągi a_n = 2nπ i b_n = (2n+1)π oba dążą do +∞ ale f(a_n) = e^2nπ*1 → +∞ natomiast f(b_n)=e{2n+1)π*(−1) → −∞ granica przy x→ −∞ istnieje i jest = 0 bo y = cosx jest ograniczona, a y=e^x →0 z powyższego wynika, że asymptot pionowych nie ma natomiast istnieje asymptota pozioma lewostronna y=0

	nπ
taka trochę nietypowa bo dla x= −		funkcja przyjmuje wartość 0
	2

ale dla pozostałych wartości y=0 jednak tą asymptotą jest 3. pochodna f'(x) = e^x*cosx − e^x*sinx = e^x(cosx−sinx) =

	x+π2−x		x−π2+x
ex(cosx − cos(π2−x) ) = ex*(−2sin		*sin		) =
	2		2

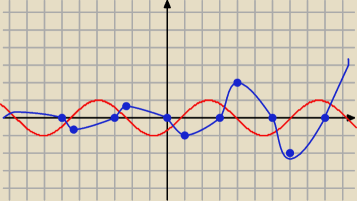
−2e^x*sin^π₄*sin(x−^π₄) = −√2e^x*sin(x−^π₄) f'(x) = 0 ⇔ sin(x−^π₄) = 0 ⇔ x−^π₄ = kπ ⇔ x = ^π₄+kπ −√2*e^x < 0 dla każdego x∊R w punktach ^π₄+2kπ sin(x−^π₄) zmienia znak z (−) na (+) czyli f'(x) zmienia znak z (+) na (−) i w tych punktach masz maksima natomiast w punktach ^π₄+(2k+1)π sin(x−^π₄) zmienia znak z (+) na (−) czyli f'(x) zmienia znak z (−) na (+) i w tych punktach masz minima to trzeba sobie odczytać z wykresu wykres (bardzo niedoskonały tej funkcji to ta niebieska krzywa) zobacz jak to narysuje wolfram

wota: a Ekstrema lokalne funkcji?

Basia: A maksima i minima to co to jest ? Psy z kulawymi łapami czy może ekstrema właśnie ?