pola trójkątów Aga: Ćwiczę zadania na sprawdzian i chyba mi się już mózg popsuł bo robię to zadanie już 2h i dalej nic mi nie wychodzi Proszę o pomoc. Na boku AC trójkąta ABC wybrano punkt D taki że AD = 3 DC. Pole trójkąta ABD jest równe 9. Oblicz Pole trójkąta ABC. Nawet coś narysowałam  http://pokazywarka.pl/tns3mg/ z twierdzenia Pitagorasa 3x² + h² = a² x² + h² = b² Z Pola ABD: 3x * h * ¹₂= 9 H = ⁶_x Po podstawieniu w dalszym ciągu mam 3 niewiadome a tylko 2 równania więc nie idzie zrobić wyrażenia algebraicznego. Podejrzewam, że to pewnie w ogóle nie powinno być tak ale już nie mam siły nad tym myśleć.

agulka:

	x		3		x
AC=x+y,		=		⇒y=
	y		1		3

P_ABD=9

	1
PABD=		*x*h
	2

	1
9=		*x*h
	2

x*h=18

	1
PABC=		*AC*h
	2

	1
PABC=		*(x+y)*h
	2

2*P_ABC=xh+yh 2*P=18+yh

	x
2*P=18+		*h /*3
	3

6*P=54+x*h 6*P=54+18 P=12

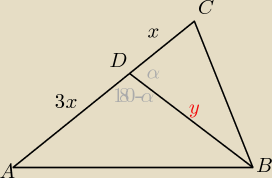Saizou : P_ABD=9

	1
9=		*3x*y *sin(180−α)
	2

18=3x*y *sinα 6=xy*sinα

	1		1
PBDC=		*x*y*sinα=		*6=3
	2		2

P_ABC=9+3=12

agulka:

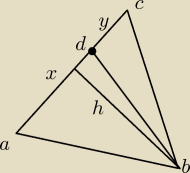
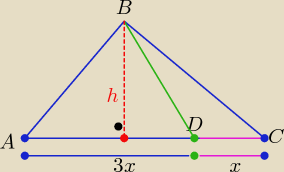aza: h jest wspólną wysokością trójkątów ADB i CDB x>0 z treści zadania |AD|= 3|DC| ⇒ |AD|=3x , |DC|= x

	3x*h		x*h
P(ADB)=		= 9 ⇒		= 3 = P(ΔCDB)
	2		2

zatem P((ABC)= P(ADC)+P(BDC)=9+3=12 [j²]

Aga: Dziękuje ślicznie Już kumam.