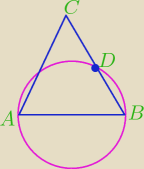
Planimetria ;/ bezendu: Dany jest trójkąt równoboczny ABC .Okrąg o średnicy AB przecina bok BC w punkcie D wykaż że |CD|=|DB| Jak to zacząć ? .

Basia: zacząć i skończyć równocześnie dorysować AD i pomyśleć jakim kątem jest ADB i co z tego wynika skoro ABC jest równoboczny

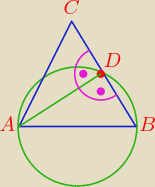
bezendu: Czyli |AD| to jest wysokość tego trójkąta

aza: taaaaaaaaaaak

bezendu: i to koniec dowodu ? ( z planimetrii jestem bardzo słaby na razie )

Basia: no cóż koniec; spodek wysokości w tr. równonocznym jest środkiem boku z czego wynika, że BD = CD

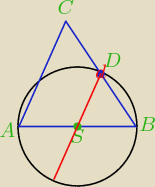
bezendu: d=2r |SD|=r |DB|=r więc |CB|=2r

Basia: oczywiście tak; AB = BC = AC = 2r

bezendu: |CD|=|BC|−|DB| 2r−r=r czyli ta średnica dzieli odcinek |CB| na równe połowy ?

bezendu:

Mila: bezendu, weź cyrkiel i linijkę. Wykonaj konstrukcję Δ równobocznego na średnicy, wszystko Ci się wyjaśni. Wysokość , środkowa pokrywają się w Δ równobocznym. Czynnościowe przyswajanie wiadomości było dawniej zalecane przez metodyków. I ja to popieram.

bezendu: Chyba tak najlepiej bo ''wirtualnie'' to tego nie widać Dziękuje i dobranoc

Mila: Dobranoc

bezendu: http://www.math.edu.pl/trojkat-rownoboczny czy oprócz tych własności są jeszcze jakieś inne które tam nie zostały podane, może jakieś inne wzory do policzenia wysokości ?