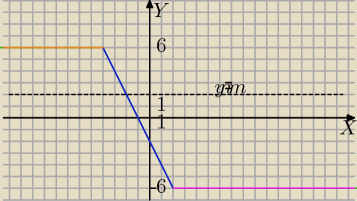
 f(x)=|x−2|−|x+4|
|x−2|=x−2 ⇔x−2≥0⇔x≥2
|x+4|=x+4⇔x+4≥0⇔x≥−4
Rozważamy jaki wzór ma funkcja w przedziałach:
1)x∊(−∞,−4)
2)x∊<−4,2)
3) x∊<2,∞)
ad 1)x∊(−∞,−4)
f(x)=−x+2−(−x−4)=−x+2+x+4⇔ f(x)=6 funkcja stała
ad2)x∊<−4,2)
f(x)=−x+2−(x+4)=−x+2−x−4⇔ −2x−2
ad 3) x∊<2,∞)
f(x)=x−2−(x+4)=x−2−x−4⇔f(x)=−6
dla m=6 lub m=−6 równanie ma nieskończenie wiele rozwiązań
{dla m∊(−6,6) jedno rozwiązanie ,a rysnku widać, że dla m=2 jedno rozwiązanie
dla m>6 brak rozwiązań
dla m<−6 brak rozwiązań
f(x)=|x−2|−|x+4|
|x−2|=x−2 ⇔x−2≥0⇔x≥2
|x+4|=x+4⇔x+4≥0⇔x≥−4
Rozważamy jaki wzór ma funkcja w przedziałach:
1)x∊(−∞,−4)
2)x∊<−4,2)
3) x∊<2,∞)
ad 1)x∊(−∞,−4)
f(x)=−x+2−(−x−4)=−x+2+x+4⇔ f(x)=6 funkcja stała
ad2)x∊<−4,2)
f(x)=−x+2−(x+4)=−x+2−x−4⇔ −2x−2
ad 3) x∊<2,∞)
f(x)=x−2−(x+4)=x−2−x−4⇔f(x)=−6
dla m=6 lub m=−6 równanie ma nieskończenie wiele rozwiązań
{dla m∊(−6,6) jedno rozwiązanie ,a rysnku widać, że dla m=2 jedno rozwiązanie
dla m>6 brak rozwiązań
dla m<−6 brak rozwiązań