matematykaszkolna.pl
Trygonometria Turkuć: Siemka WIedząc , że
 2 3 5 
tgα=
,α∊(π;
π) , oblicz sin(2α+
π)
 3 2 4 
28 maj 19:54
Beti: a znasz wynik?
28 maj 20:16
aza: Mnie wyszło:
 17√2 
−
 26 
28 maj 20:19
Beti: mnie też, więc obliczenia są OK emotka
28 maj 20:21
krystek: sin2αcos225+sin225cos2α=.. i dalej rozpisać
 2 3 
wiedząc ,ze sinα=−
cosα=−
 13 13 
28 maj 20:21
aza: Ejj krystek
 2 3 
sinα= −
, cosα= −
 √13 √13 
28 maj 20:23
Beti: raczej:
 2 3 
sinα = −
i cosα = −
 √13 √13 
28 maj 20:23
aza: emotka
28 maj 20:24
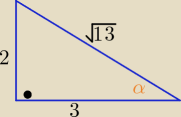
aza: rysunek α∊IIIćw. ⇒ sinα<0 i cosα<0
 2 3 
sinα= −
i cosα= −
 √13 √13 
 π π π π 
sin(2α+π+
)= − sin(2α+
)= −(sin2α*cos
+cos2α*sin
)=
 4 4 4 4 
 √2 √2 
= −
(sin2α+cos2α)= −
( 2sinαcosα+cos2α−sin2α)=
 2 2 
 √2 6 9 4 17√2 
= −
( 2*
+
−
)= −
 2 13 13 13 26 
28 maj 20:31
krystek: Dzieki@aza za zwrócona uwagę , oczywiście zjadłam na kolacje pierwiastek
28 maj 20:33
aza: emotka
28 maj 20:36
krystek: Oj aza emotka emotka
28 maj 20:37
aza:
28 maj 20:37
Turkuć: Dzięki
28 maj 20:47
aza: No emotka
28 maj 20:48