Matura próbna 2013
bezendu:
Dziś w mojej szkole odbyła się próbna matura z matematyki, wstawię to swoje rozwiązania i
proszę niech ktoś sprawdzi wyniki i zapis

Zadanie 1(1pkt)
15% liczby x jest równe 30. Wynika stąd, że:
x−100%
A) x=2 B) x=45 C) x=200 D) x=450
x=200
Zadanie 2 (1pkt)
Z faktu, że liczba 15 to p% liczby 120 wynika, że
120−100%
15−x%
A) p<3 B) p=8 C) p=10 D) p>10
p>10
Zadanie 3 (1pkt)
Iloraz 4
8:8
4 jest równy:
| (22)8 | | 216 | |
| = |
| =216−212=24 |
| (23)4 | | 212 | |
A) 1 B) 2
−4 C) 2
4 D) 4
4
24
28 maj 14:48
bezendu:

Zadanie 4 (1pkt)
Wskaż nierówność która opisuję sumę przedziałów
A) |x−1|<3 B) |x−1|>3 C) |x+1|<3 D) |x+1|>3
|x−1|>3
x−1>3 lub x−1<−3
x>4 lub x<−2
|x−1|>3
28 maj 14:52
bezendu:
Zadanie 5 (1pkt)
Liczba 2log6 jest równa
A) log36 B) log12 C) log8 D) log4
log36
Zadanie 6 (1pkt)
Z faktu, że funkcja liniowa f(x)=(3−m)x+4 jest malejąca wynika, że
3−m<0
−m<−3
m>3
m∊(3,∞)
A) m∊(−∞,4) B) m=−4 C) m=3 D) m∊(3,∞)
Zadanie 7 (1pkt)
Liczba 2 jest miejscem zerowym funkcji liniowej f(x)=(m−1)x−4
(m−1)*2−4=0
2m−2−4=0
2m=6
m=3
A) m=−1 B) m=1 C) m=3 D) m=−3
m=3
28 maj 14:59
bezendu:
Zadanie 8
Wyrażenie 4x2−6 jest równe iloczynowi
4x2−6
(2x−√6)(2x+√6)
A) (2x−2)(2x+2) B) (4x+√3)(4x−√3) C) (2x−√6)(2x+√6) D) (4x−1)(x+6)
(2x−√6)(2x+√6)
Zadanie 9 (1pkt)
Wierzchołek paraboli o równaniu y=(x−3)2+2 ma współrzędne
A) (3,2) B) (3,−2) C) (−3,2) D) (−3,−2)
(3,2)
28 maj 15:04
bezendu:
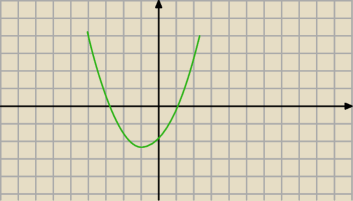
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej. f(x)=ax
2+bx+c Wynika stąd, że
A) a>0 i c>0
B) a>0 i c<0
C) a<0 i c>0
D) a<0 i c<0
a>0 i c<0
28 maj 15:09
bezendu:
Zadanie 11 (1pkt)
Zbiorem rozwiązanie nierówności 3(x+2)(x−1)<0 jest
A) (−2,1) B) (−1,2) C) (−∞,−2)∪(1,∞) D) (−∞,−1)∪(2,∞)
(−2,1)
Zadanie 12 (1pkt)
Dla n=1,2,3... ciąg określony jest wzorem an=(−2)n(4−n) Wtedy.
A) a3<1 B) a3=1 C) a3=8 D) a3>8
a3=(−2)3*(4−3)
a3=−8
a3<1
28 maj 15:16
bezendu: Zadanie 13 (1pkt)
W ciągu arytmetycznym (a
n) dane są a
3=8 i a
5=16. Wynika stąd, że
A) a
2=−4 B) a
2=0 C) a
2=4 D) a
2=12
a
1+2r=8 /(−1)
a
1+4r=16
−a
1−2r=−8
a
1+4r=16
2r=8
r=4
a
1+8=8
a
1=0
a
n=(n−1)*4
a
2=(2−1)*4
a
2=4
a2=4
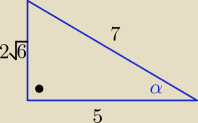
Zadanie 14 (1pkt)
| | 5 | |
Kąt α jest ostry i cosα= |
| . Wynika stąd, że sinα |
| | 7 | |
| | 2 | | 2√6 | | 2√6 | | 5 | |
A) |
| B) |
| C) |
| D) |
| |
| | 7 | | 7 | | 5 | | 2√6 | |
sin
2α+cos
2α=1
28 maj 15:26
bezendu:
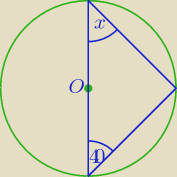
Zadanie 15 (1pkt)
Zaznaczony na rysunku (punkt 0 to środek okręgu) kąt x jest równy
A) 30
o B) 40
0 C) 50
0 D) 60
o
50o
28 maj 15:32
aza:
Można krótko:
a
2= a
3−r=... = 4
28 maj 15:33
aza:
28 maj 15:35
bezendu:
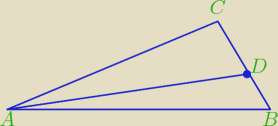
Zadanie 16 (1pkt)
Pole trójkąta ABC jest równe 36 Punkt D leży na boku BC i |BC|

DC|=1:3.Pole trójkąta ABD jest
równe:
A) 4 B) 6 C) 9 D 12
12
28 maj 15:36
bezendu: @azz nie chodzi mi o sposób tylko wyniki

ale poczekaj aż wstawię wszystko
28 maj 15:37
bezendu:
Zadanie 17 (1pkt)
| | 7x | |
Dziedziną wyrażenia |
| jest |
| | x3+2x2−4x−8 | |
x
3+2x
2−4x−8≠0
x
2(x+2)−4(x+2)≠0
(x+2)(x
2−4)≠0
(x+2)(x−2)(x+2)≠0
D
f=R\{−2,2}
A) R\{−2,2} B) R\{−2} C) R\{−2,0} D) R
Zadanie 18 (1pkt)
A={1,2,3,4,5} B={1,2,6,7} A∪B wynosi ?
A∪b={1,2,3,4,5,6,7}
28 maj 15:44
bezendu: Zadanie 19 (1pkt)
| | 4 | |
Wskaż równanie prostej prostopadłej do prostej y= |
| x−3 |
| | 3 | |
Zadanie 20 (1pkt)
−6−2√5
Zadanie 21 (1pkt)
Punkty A=(2,−1) i B=(4,3) są wierzchołkami trójkąta równobocznego ABC. Długośc boku tego
trójkąta wynosi
2√5
28 maj 15:51
bezendu:
Zadanie 22 (1pkt)
Punkty A=(5,2) C=(1,4) są przeciwległymi wierzchołkami prostokąta ABCD. Środek okręgu opisanego
na tym prostokącie ma współrzędne
(3,3)
Zadanie 23(1pkt)
Objętość sześcianu jest równa 64cm3. Suma długości wszystkich krawędzi tego sześcianu jest
równa
48cm
Zadanie 24 (1pkt)
Wartość wyrażenia W=|x−6|−3x+5 dla x∊(0,6) jest równa
−4x+11
Zadanie 25 (1pkt)
Dana jest funkcja kwadratowa f(x)=x2−8x−5. Funkcja jest rosnąca w przedziale
<4,∞)
28 maj 16:05
bezendu:
Zadania otwarte
Zadanie 26 (2pkt)
Rozwiąż nierówność
x
2+x−12<0
Δ=49
√Δ=7
x∊(−4,3)
Zadanie 27( 2pkt)
Rozwiąż równanie x
3−3x
2−4x+12=0
x
2(x−3)−4(x−3)=0
(x−3)(x
2−4)=0
(x−3)(x−2)(x+2)=0
x=3 lub x=2 lub x=−2
28 maj 16:12
aza:
Jak do tej pory , to

28 maj 16:24
bezendu:
Zadanie 28 (2pkt)
Wyznacz równanie symetralnej odcinka AB gdy A=(−2,1) B=(6,3)
| | −2+6 | | 1+3 | |
S= |
| , |
| }=(2,2) |
| | 2 | | 2 | |
−2a+b=1 /(−1)
6a+b=3
2a−b=−1
6a+b=3
8a=2
y=−4x+b
−4*2+b=2
−8+b=2
b=10
y=−4x+10
28 maj 16:29
bezendu:
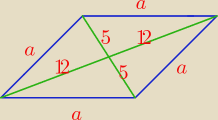
Zadanie 29 (2pkt)
Przekątne rombu mają długość 10 cm i 24 cm. Oblicz wysokość tego rombu
5
2+12
=x
2
25+144=x
2
x
2=169
x=13 lub x=−13 (bok nie może być ujemny więc odrzucam rozwiązanie ujemne )
a=13
P=120
P=ah
120=13h
28 maj 16:36
Mati_gg9225535:
w zad. 16 ten stosunek odcinków jest w porządku podany?
28 maj 16:38
asdf: niezdałbym

28 maj 16:40
aza:

28 maj 16:41
bezendu: Zadanie 30 (2pkt)
| | 4sinα−cosα | |
Kąt α jest ostry i tgα=3. Oblicz |
| |
| | sinα+3cosα | |
tgα=3
tgα*ctgα=1
3cosα=sinα
i dalej nie zrobiłem może 1 punkt chociaż będzie

28 maj 16:43
bezendu: Zadanie 16 poprawka |BD| : |DC|=1:3
28 maj 16:44
aza:
zad30)
wystarczyło podzielić licznik i mianownik przez cosα≠0
| | 4tgα−1 | | 12−1 | |
W= |
| = |
| =..... |
| | tgα+3 | | 3+3 | |
28 maj 16:45
bezendu: Zadanie 31 (2pkt)
| | m+1 | | m+3 | | m+9 | |
Wykaż, że dla każdego m ciąg ( |
| , |
| , |
| ) jest arytmetyczny |
| | 4 | | 6 | | 12 | |
| | m+10−m−9 | | 1 | |
an+1−an= |
| = |
| |
| | 12 | | 12 | |
C.N.D
28 maj 16:51
aza:
zad 31/ 2sposób
a,b,c −− tworzą ciąg arytmetyczny ⇒ 2b= a+c
L=P
c.n.w
28 maj 16:59
bezendu: Zadanie 32 (4pkt)
ciąg (9,x,19) jest ciągiem arytmetycznym a ciąg (x,42,y,z) Oblicz x,y,z
x−9=19−x
2x=28
x=14
(14,42,y,z)
y=42*3=126
z=126*3=378
28 maj 17:01
bezendu: @aza a moje rozwiązanie jest złe

28 maj 17:01
bezendu: Zadanie 33 (5pkt)
W pewniej szkole maturzyści mieli zapłacić za salę i muzykę na bal studniówkowy w sumie 16500
zł. Gdyby 10 osób nie poszło na studniówkę, każdy z pozostałych musiałby zapłacić o 15 zl
więcej. Oblicz, ilu maturzystów jest w tej szkole.
rozwiązałem taki układ równań
xy=16500
(x−10)(y+15)=16500
wyszło 110 maturzystów
To już było ostatnie zadanie

28 maj 17:06
aza:
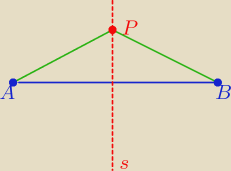
zad 28/ 2 sposób
Każdy punkt należący do symetralnej odcinka, jest równo oddalony od końców tego odcinka
P(x,y) |AP|
2= |BP|
2
(x+2)
2+(y−1)
2= (x−6)
2+(y−3)
2
.............................
16x+4y=40 / :4
s :
y= −4x+10
28 maj 17:06
aza:
@bezendu
Wszystkie są bardzo dobre! ( gratuluję wiedzy
Podaję jedynie jeszcze inne sposoby rozwiązania( może się komuś przydadzą?
28 maj 17:09
bezendu: a zadanie 16 też jest ok

i jeszcze jedno za zadanie 30 mogę sobie policzyć 1 punkt czy 0

28 maj 17:10
aza:
W zad.33
Czy podałeś odpowiednie założenia i oznaczenia?
x∊N+ , y∊R+
28 maj 17:11
bezendu: w zadaniu 33 napisałem tylko x−liczba maturzystów y−ilość pieniędzy nie napisałem założeń

28 maj 17:12
bezendu: ale jak wyszedł pierwiastek ujemny −100 to napisałem, że odrzucam ponieważ liczba maturzystów
nie może być ujemna

28 maj 17:16
aza:
zad.16 P= 9 odp C) przykro mi
28 maj 17:18
aza:
Na przyszłość
pamiętaj o takich założeniach

28 maj 17:19
bezendu: 
czyli podsumowując jedno zadanie źle i jedno nie dokończone czyli 94 % jeśli reszta jest ok
?
28 maj 17:20
bezendu: Dobrze i dziękuje za sprawdzenie

28 maj 17:20
aza:
Gratuluję

i pozdrawiam od Ety

28 maj 17:22
bezendu: Eta 
28 maj 17:23
aza:

28 maj 17:24
bezendu: W piątek wstawię poziom rozszerzony

28 maj 17:24
aza:
ok

28 maj 17:26
asdf: @bezendu
zad 16: przypomnij sobie jak wyprowadzałeś wzór na tg2x..tu dosłownie to samo trzeba było
zrobić
28 maj 17:39
bezendu: @asdf zadanie 16 jest z trójkątem

a wzór to do ścisłości wyprowadzałeś Ty

28 maj 17:40
asdf: | | cosx | |
o 30 mi chodzilo, oj tam ja od razu..ja tylko podzieliłem przez |
| , ty zrobiles |
| | cosx | |
reszte.
28 maj 17:46
bezendu:
sinα=3cosα
| 4(3cos)−cosα | | 12cosα−cosα | | 11cosα | | cosα(11) | |
| = |
| = |
| = |
| = |
| 3cosα+3cosα | | 6cosα | | 6cosα | | cosα(6) | |
28 maj 17:50
aza:
| | 11 | |
Zobacz wpis16:45 ..= |
| |
| | 6 | |
28 maj 17:54
bezendu: za dwa tygodnie jak będzie podobne zadanko to już będę wiedział

28 maj 17:56
Cusack: co do 31, tak się składa że też miałem u siebie na próbnej maturze to zadanie.
ono jest z arkusza listopad 2009.
zrobiłem jak
aza i zero punktów

a to dlatego, że to twierdzenie jest dla ciągu arytmetycznego, a my na początku nie wiemy czy
to jest ciąg arytmetyczny... tylko mamy to udowodnić, tak jak zrobił to
bezendu
28 maj 18:45
bezendu: 
28 maj 18:47
28 maj 18:53
Mila:
bezendu, całkiem ładnie, ale to dla Ciebie proste zadania. Straty małe. Gratuluję.

Na rozszerzonym są trudniejsze, zobacz arkusze OKE−Lublin
28 maj 18:54
bezendu: poziom rozszerzony pisze w piątek ale tam już tak dobrze nie pójdzie

Od czego najlepiej
powtórzyć planimetrię a raczej jak jej się dobrze nauczyć

28 maj 18:59
Cusack: @aza, jak to się ma do tego co napisałem?

28 maj 19:24
Mila: Popatrz na zadania − Próbne matury dla klas drugich, OKE− Poznań, Lublin, Bydgoszcz.
Tam są naprawdę dobre zadania.
28 maj 19:26
bezendu:
Już pościągałem sobie arkusze i robię codziennie+zadania z kiełbasy ale w tych zadaniach z
planimetrii wychodzą moje braki (np nie znajomość tw sinusów i kosinusów ) więc zanim się
zabiorę za te zadani chcę mieć dobrze opanowane podstawy

28 maj 19:31
Mila: W Kiełbasie też są dobre zadania z planimetrii, niektóre dość trudne, może za trudne dla Ciebie
w tym momencie edukacji.
Powodzenia, wpisuj problemy.
28 maj 19:38
bezendu: Dziękuje na razie staram się jeszcze poczytać i samemu próbować robić jak nie będę wiedział to
będę prosił o wskazówki

28 maj 19:40
5 cze 16:03
Cusack:
hmm...
jak dla mnie, niepotrzebnie liczyłeś wszędzie a
n+1
| | m+1 | | m+3 | |
skoro an= |
| , to an+1= |
| , bo tak jest podane... |
| | 4 | | 6 | |
5 cze 16:14
bezendu: @Cusack a czytałeś swój post 28 maja 18:45 ?

5 cze 16:15
Cusack: btw, u mnie większość osób poległa na tym zadaniu (ja również) stosując wzór
5 cze 16:16
Cusack: niestety spojarzałem tylko na sposób, tj. an+1 − an
na same liczby nie patrzyłem.
sory.
5 cze 16:18
bezendu:
Ale przecież każde rozwiązanie prowadzące do wyniku jest poprawne...Nie rozumiem wykazałem
przecież że dla każdego m jest arytmetyczny coś tu nie gra

5 cze 16:18
Cusack: co miałeś na myśli pisząc, że:
| | 1 | |
an+1 − an = |
| jest arytmetyczny |
| | 4 | |
i niżej to samo
5 cze 16:21
bezendu:
wykazałem że dla każdego m z tego przedziału ciąg jest arytmetyczny..
5 cze 16:23
Cusack: może źle się wyraziłem
zeby ciag byl arytmetyczny to roznica musi byc stała.
u Ciebie są trzy różne
5 cze 16:24
bezendu: czyli ostatecznie to jest źle

5 cze 19:10
Eta:
To co ja napisałam jest dobrze!
w ciągu tym są podane trzy kolejne wyrazy!
5 cze 23:27
bezendu: no tak ale jak ja wstawiłem swoje rozwiązanie to mówiłaś że jest ok i pokazałaś inny sposób a
tu proszę...
5 cze 23:28
Eta:
Wtedy źle spojrzałam

5 cze 23:33
5 cze 23:36
bezendu: 
5 cze 23:36
bezendu: widziałem to rozwiązanie i rozwiązanie podawane przez OKE i tam niestety nie ma mojej metody

5 cze 23:37
ZKS:
| | m + 1 | | m + 1 + 1 | |
bezendu skoro masz podane an = |
| to nijak an + 1 ≠ |
| |
| | 4 | | 4 | |
masz tam gdzieś
n?
5 cze 23:37
Eta:
Jak nie, to nie!

5 cze 23:38
bezendu: ZKS nie mam
5 cze 23:39
ZKS:
Przecież m to jakaś stała a żeby policzyć an + 1 tak jak Ty to zrobiłeś to musiało
by an być uzależnione od zmiennej n.
5 cze 23:39
Eta:
Witam
ZKS 
Przed sekundą napisałam to samo , ale nie poszło

(echh... nie ten klawisz nacisnęłam
5 cze 23:40
bezendu: Dobra już wiem gdzie błąd mam dziękuje i dobranoc

5 cze 23:41
ZKS:
Chociaż mój mózg dzisiaj już nie pracuje po tym całym tygodniu na uczelni więc może się mylę.
5 cze 23:41
bezendu: Eta post 23:36 był odpowiedzią na Twój post 22:33 a nie że nie chcę zajrzeć do rozwiązania
Jakuba

5 cze 23:42
ZKS:
Witaj
Eta.


5 cze 23:43
Mila:
Bezendu, ja badam zawsze z definicji⇔
dla ciągu 3 −wyrazowego: czy
a2−a1=a3−a2 to jest sposób równoważny z tym, co podała Eta.
Dla ciągu podanego wzorem ogólnym:
czy :
an+1−an jest wielkością stałą.
5 cze 23:47
Eta:
A ja tak:
a,b,c −− kolejne wyrazy ciągu arytmetycznego ⇒ 2b=a+c
a,b,c −−− kolejne wyrazy ciągu geometrycznego ⇒ b2= a*c
5 cze 23:51
 Zadanie 1(1pkt)
15% liczby x jest równe 30. Wynika stąd, że:
Zadanie 1(1pkt)
15% liczby x jest równe 30. Wynika stąd, że:
 Zadanie 4 (1pkt)
Wskaż nierówność która opisuję sumę przedziałów
A) |x−1|<3 B) |x−1|>3 C) |x+1|<3 D) |x+1|>3
|x−1|>3
x−1>3 lub x−1<−3
x>4 lub x<−2
|x−1|>3
Zadanie 4 (1pkt)
Wskaż nierówność która opisuję sumę przedziałów
A) |x−1|<3 B) |x−1|>3 C) |x+1|<3 D) |x+1|>3
|x−1|>3
x−1>3 lub x−1<−3
x>4 lub x<−2
|x−1|>3
 Na rysunku przedstawiono fragment wykresu funkcji kwadratowej. f(x)=ax2+bx+c Wynika stąd, że
A) a>0 i c>0
B) a>0 i c<0
C) a<0 i c>0
D) a<0 i c<0
a>0 i c<0
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej. f(x)=ax2+bx+c Wynika stąd, że
A) a>0 i c>0
B) a>0 i c<0
C) a<0 i c>0
D) a<0 i c<0
a>0 i c<0
 Zadanie 15 (1pkt)
Zaznaczony na rysunku (punkt 0 to środek okręgu) kąt x jest równy
A) 30o B) 400 C) 500 D) 60o
50o
Zadanie 15 (1pkt)
Zaznaczony na rysunku (punkt 0 to środek okręgu) kąt x jest równy
A) 30o B) 400 C) 500 D) 60o
50o

 Zadanie 16 (1pkt)
Pole trójkąta ABC jest równe 36 Punkt D leży na boku BC i |BC|
Zadanie 16 (1pkt)
Pole trójkąta ABC jest równe 36 Punkt D leży na boku BC i |BC| DC|=1:3.Pole trójkąta ABD jest
równe:
A) 4 B) 6 C) 9 D 12
12
DC|=1:3.Pole trójkąta ABD jest
równe:
A) 4 B) 6 C) 9 D 12
12
 ale poczekaj aż wstawię wszystko
ale poczekaj aż wstawię wszystko

 Zadanie 29 (2pkt)
Przekątne rombu mają długość 10 cm i 24 cm. Oblicz wysokość tego rombu
Zadanie 29 (2pkt)
Przekątne rombu mają długość 10 cm i 24 cm. Oblicz wysokość tego rombu





 zad 28/ 2 sposób
Każdy punkt należący do symetralnej odcinka, jest równo oddalony od końców tego odcinka
P(x,y) |AP|2= |BP|2
(x+2)2+(y−1)2= (x−6)2+(y−3)2
.............................
16x+4y=40 / :4
s : y= −4x+10
zad 28/ 2 sposób
Każdy punkt należący do symetralnej odcinka, jest równo oddalony od końców tego odcinka
P(x,y) |AP|2= |BP|2
(x+2)2+(y−1)2= (x−6)2+(y−3)2
.............................
16x+4y=40 / :4
s : y= −4x+10
 i jeszcze jedno za zadanie 30 mogę sobie policzyć 1 punkt czy 0
i jeszcze jedno za zadanie 30 mogę sobie policzyć 1 punkt czy 0 



 czyli podsumowując jedno zadanie źle i jedno nie dokończone czyli 94 % jeśli reszta jest ok
?
czyli podsumowując jedno zadanie źle i jedno nie dokończone czyli 94 % jeśli reszta jest ok
?

 i pozdrawiam od Ety
i pozdrawiam od Ety 




 a wzór to do ścisłości wyprowadzałeś Ty
a wzór to do ścisłości wyprowadzałeś Ty 

 a to dlatego, że to twierdzenie jest dla ciągu arytmetycznego, a my na początku nie wiemy czy
to jest ciąg arytmetyczny... tylko mamy to udowodnić, tak jak zrobił to bezendu
a to dlatego, że to twierdzenie jest dla ciągu arytmetycznego, a my na początku nie wiemy czy
to jest ciąg arytmetyczny... tylko mamy to udowodnić, tak jak zrobił to bezendu

 Na rozszerzonym są trudniejsze, zobacz arkusze OKE−Lublin
Na rozszerzonym są trudniejsze, zobacz arkusze OKE−Lublin
 Od czego najlepiej
powtórzyć planimetrię a raczej jak jej się dobrze nauczyć
Od czego najlepiej
powtórzyć planimetrię a raczej jak jej się dobrze nauczyć 











 Przed sekundą napisałam to samo , ale nie poszło
Przed sekundą napisałam to samo , ale nie poszło  (echh... nie ten klawisz nacisnęłam
(echh... nie ten klawisz nacisnęłam



