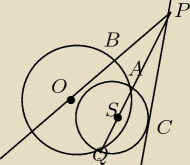
Oblicz franek499: Okręgi o środkach O i S przecinają się w punktach A i Q i punkt S należy do cięciwy AQ. Punkt P leży na prostej AQ, prosta PC jest styczną do okręgu o środku S (w punkcie C), punkt B jest punktem przecięcia odcinka PO z okręgiem o środku O(rysunek). Wiedząc, że |PA|= 8cm, |PB|= 6cm i |PC|= 12 cm, oblicz |OS|. wynik ma być: 2√14

+-: Dwa razy twierdzenie o siecznych i mamy średnice 5 i 9, następnie z Pitagorasa OS=2√14

irena_1: Średnice mają długości 10 i 18. To promienie mają długości 5 i 9...