geometria xantor: W trójkącie dwa boki mają długości 12 i 3, kąt między nimi jest równy 60 stopni a ole wynosi 9 pierwiastków z 3. Oblicz : a) promień okręgu opisanego na tym trójkącie b) promień okręgu wpisanego w ten trójkąt Proszę bez twierdzeń sinusów itp.

Mila: I co jest równe 9√3, pole Δ?

xantor: nom pole

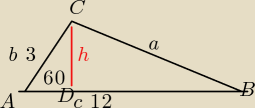
Mila: W trójkącie dwa boki mają długości 12 i 3, kąt między nimi jest równy 60 stopni . Oblicz : a) promień okręgu opisanego na tym trójkącie b) promień okręgu wpisanego w ten trójką P=9√3

	abc
P=
	4R

	1
P=p*r, p=		(a+b+c)
	2

W ΔADC:

	1
AD=		*3=1,5
	2

	3√3
h=
	2

|DB|=12−1,5=10,5 h²+DB²=a²

	3√3
(		)2+10,52=a2
	2

	27		1
a2=		+110
	4		4

a²=117 a=√117=√9*13 a=3√13

	1
9√3=		*(3+12+3√13)*r
	2

18√3=(15+3√13)*r

	18√3
r=
	3*(5+√13)

	6√3
r=		− promień okręgu wpisanego w Δ
	5+√13

Usuń niewymierność z mianownika 2) Promień okręgu opisanego na Δ

	3*12*3√13
9√3=
	4R

9√3*4R=9*12√13 √3*4R=12√13

	3√13
R=
	√3

R=√39

xantor: wielkie dzięki Mila

Mila: