Zadanie Ona_18: Dwa boki równoległoboku zawarte są w prostych o równaniach: y−2=0 2x=y+14 a jego przekątne przecinają się w punkcie S=(3,−1).Wyznacz: a)równania pozostałych boków tego równoległoboku b) współrzędne wierzchołków równoległoboku.

AS:

	1
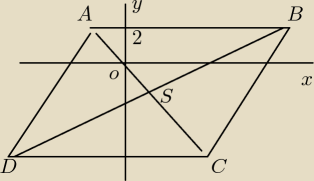
Równanie prostej AD: y =		*x +7
	2

Równanie prostej AB: y = 2 Punkt przecięcia przekątnych: S(3,−1) Rozwiązanie: 1. Wsp. punktu A Rozwiązuje układ równań

	1
y =		*x + 7 i y = 2
	2

	1
2 =		*x + 7 ⇒ x = −3
	2

Punkt A(−3,2) 2. Wsp. punktu C S − środek odcinka AC

xA + xC		−3 + xC
	= xS ⇒		= 3 ⇒ xC = 9
2		2

yA + yC		2 + yC
	= yS ⇒		= −1 ⇒ yC = −4
2		2

Punkt C(9,−4) 3. Równanie prostej CD y = −4 4. Równanie prostej BC y − yC = m*(x − xC) m − wsp. kierunkowy prostej AD

	1		1		17
y + 4 =		*(x −9) ⇒ y =		*x −
	2		2		2

5. Punkt B

	1		17
y =		*x −		y = 2
	2		2

	1		17
2 =		*x −		⇒ x = 21
	2		2

B(21,2) 6. Punkt D

	1
y =		*x + 7 y = −4
	2

	1
−4 =		*x + 7 ⇒ x = −22
	2

D(−22,−4)