help :): rozwiąż równanie: x(|x|+|2x−3|)=4 . ?

Mila: x(|x|+|2x−3|)=4 |x|=x dla x≥0

	3
|2x−3|=2x−3 ⇔x≥
	2

1)D=(−∞,0) |x|=−x, |2x−3|=−2x+3 x(−x−2x+3)=4 x(−3x+3)−4=0 −3x²+3x−4=0 Δ=9−4*(−3)*(−4)=9−48<0 brak rozwiązań

	3
2)D=<0,		)
	2

|x|=x i |2x−3|=−2x+3 x*(x−2x+3)−4=0 x(−x+3)−4=0 −x²+3x−4=0 Δ=9−4*(−1)*(−4)=9−16<0 brak rozwiązań

	3
3) D=<		,∞)
	2

x(x+2x−3)−4=0 x(3x−3)−4=0 3x²−3x−4=0 Δ=9+4*3*4=9+48=57

	3−√57		3+√57
x1=		<0∉D lub x2=
	6		6

	3+√57		3
czy		>		? /*6
	6		2

3+√57>?9 √57>?6 tak odp.

	3+√57
x=
	6

:): jest gdzies błą, powinno wyjśc−1 oraz 2√2

:): jest gdzieś błąd, powinno wyjśc −1 oraz 2√2−1 <poprawiam>

Mila: Zobacz, czy dobrze zapisałaś równanie . Ja rozwiązałam takie x(|x|+|2x−3|)=4 (−1) nie może być rozwiązanie bo lewa strona wtedy jest ujemna a prawa dodatnia.

:): hm no nie wiem wtedy co jest

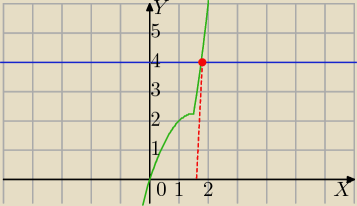
Mila: x(|x|+|2x−3|)=4 Graficznie: f(x)=x(|x|+|2x−3|) g(x)=4

	3+√57		3+7,6
x=		≈		≈1,76
	6		6