 Rysunek do zadania 8! (zaznaczony kąt wynosi 30)
Proszę o pomoc w rozwiązaniu tych zadań. Potrzebuję tego na dziś. Będę bardzo wdzięczna.
1. W trójkącie prostokątnym jedna z przyprostokątnych jest dwa razy krótsza od
przeciwprostokątnej. Wyznacz wartości funkcji trygonometrycznych kąta leżącego naprzeciw tej
przyprostokątnej.
2.Rozwiąż równania:
a)12(x−7)2(x2−8x+7)=0
b)(x2−9)(x2+5x+6)=0
3. Rozwiąż równanie x=2∥x+3∥−3 (chodzi tu o zwykłą wartość bezwzględną nie mogłam znaleźć
bardziej zbliżonego symbolu)
4. Sprawdź, że dla tych kątów, dla których tg alfa istnieje, zachodzi równość:
1+tg2alfa=1cos2alfa
5.Rozwiąż równania:
a)(x−1)2(x+3)x=0
b)x3−4x2+x+6=0
c)x4−x2−12=0
6. Sprawdź czy poniższa równość jest tożsamością trygonometryczną.
(1+sin alfa)(1cos alfa−tg alfa)=cos alfa
7. Rozwiąż nierówność ∥4x−8∥>2 (tak jak wyżej jest to zwykła wartość bezwzględna)
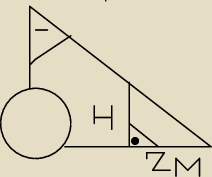
8. Oblicz wysokość podpory żurawia. Wynik podaj z dokładnością do 0.1 m.
Rysunek do zadania 8! (zaznaczony kąt wynosi 30)
Proszę o pomoc w rozwiązaniu tych zadań. Potrzebuję tego na dziś. Będę bardzo wdzięczna.
1. W trójkącie prostokątnym jedna z przyprostokątnych jest dwa razy krótsza od
przeciwprostokątnej. Wyznacz wartości funkcji trygonometrycznych kąta leżącego naprzeciw tej
przyprostokątnej.
2.Rozwiąż równania:
a)12(x−7)2(x2−8x+7)=0
b)(x2−9)(x2+5x+6)=0
3. Rozwiąż równanie x=2∥x+3∥−3 (chodzi tu o zwykłą wartość bezwzględną nie mogłam znaleźć
bardziej zbliżonego symbolu)
4. Sprawdź, że dla tych kątów, dla których tg alfa istnieje, zachodzi równość:
1+tg2alfa=1cos2alfa
5.Rozwiąż równania:
a)(x−1)2(x+3)x=0
b)x3−4x2+x+6=0
c)x4−x2−12=0
6. Sprawdź czy poniższa równość jest tożsamością trygonometryczną.
(1+sin alfa)(1cos alfa−tg alfa)=cos alfa
7. Rozwiąż nierówność ∥4x−8∥>2 (tak jak wyżej jest to zwykła wartość bezwzględna)
8. Oblicz wysokość podpory żurawia. Wynik podaj z dokładnością do 0.1 m.
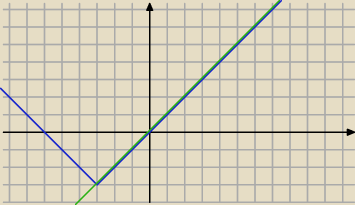 Zadanie 3 x∊<−3 ; ∞)
Zadanie 3 x∊<−3 ; ∞)
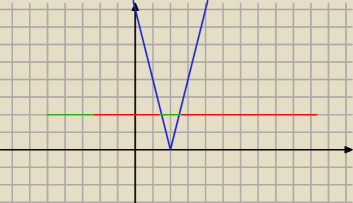 Zadanie 7. x∊(−∞ ; 1,5)∪(2,5 ; ∞)
Zadanie 7. x∊(−∞ ; 1,5)∪(2,5 ; ∞)
| sinα | sin2α | |||
4) Korzystam ze wzorów: tgα= | , tg2α= | , sin2α+cos2α=1 | ||
| cosα | cos2α |
| sin2α | cos2α+sin2α | 1 | ||||
L=1+tg2α=1+ | = | = | =P | |||
| cos2 | cos2 | cos2α |
| 1 | 1 | sinα | 1−sinα | |||||
L=(1+sinα)( | −tgα)=(1+sinα)( | − | )=(1+sinα)( | )= | ||||
| cosα | cosα | cosα | cos |
| 1−sin2α | cos2α | |||
= | =cosα=P | |||
| cosα | cosα |