Jednokładność Kun: Okrąg F1(x−3)²+(y−2)⁼9 o równaniu jest obrazem okręgu o promieniu 1 w jednokładności o środku w punkcie P(3,−1) . Wyznacz równanie okręgu F (rozpatrz dwa przypadki)

Kun: EDIT : Okrąg F1(x−3)²+(y−2)²=9 *

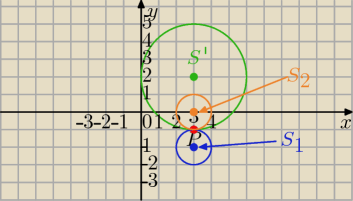
Mila: F1: (x−3)²+(y−2)²=9 S'=(3,2) , R=3 F: (x−a)²+(y−b)²=1 S=(a,b) , r=1

	3
F1 jednokładny do F względem P(3,−1) w skali k, gdzie |k|=		=3
	1

stąd k=3 lub k=−3 Z def. jednokładności: PS'^→=k*PS^→ PS^→=[a−3,b+1] PS'^→=[3−3,2+1]=[0,3] k=−3 [0,3]=−3*[a−3,b+1]⇔[0,3]=[−3a+9,−3b−3]⇔−3a+9=0 i −3b−3=3 a=3 i b=−2 S₁=(3,−2) F: (x−3)²+(y+2)²=1 dla k=3 [0,3]=3*[a−3,b+1]⇔[0,3]=[3a−9,3b+3]⇔ 3a−9=0 i 3b+3=3 a=3 i b=0 S₂=(3,0) (x−3)²+y²=1