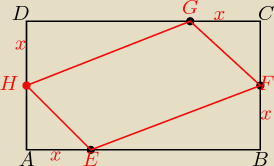
funkcja kwadratowa Monika: Dany jest prostokąt ABCD, w którym |AB| = |CD|= 22 i |BC|= |AD| = 10. Punkt E należy do boku AB, punkt F, należy do boku BC, punkt G należy do boku CD, punkt H należy do boku AD i |AD| = |BF| =|CG| = |DH|= x, gdzie x∊(0;10). Oblicz wartość x, dla której czworokąt EFGH ma najmniejsze pole.

Basia: P = P_ABCD − P_EAH − P{EBF} − P_FCG − P_GDH =

	x*(10−x)		x(22−x)		x(10−x)		x(22−x)
10*22 −		−		−		−		=
	2		2		2		2

220 − x(10−x) − x(22−x) = 220 − 10x + x² − 22x + x² P(x) = 2x² − 32x + 220 wartość najmniejszą wskazuje wierzchołek paraboli

Monika: DZIĘKI WIELKIE!