zadania maturalne,potrzebuję na jutro rozwiązania Basia: 1.Napisz równanie okręgu o środku S=(2,−4) stycznego do okręgu o podanym równaniu: (x−4)² + (y+4)²=1 2.Wyznacz wartość parametru m tak, aby prosta 3x+5y+7=0 była prostopadła do prostej o podanym równaniu m² x−(m+10)y+2=0 3. Dany jest sześciokąt foremny. Oblicz jego pole wiedząc że: krótsza przekątna tego sześciokąta ma dł.√3 3 cm. 4. Oblicz, zakładając że log₁₂ 2=a, log₆ 2

Basia: ad.1 S₁=(4;−4) r₁ = 1 |SS₁| = √(4−2)²+(−4+4)² = √4=2 r+r₁ = |SS₁| r + 1 = 2 r = 1 i napisz równanie okręgu, w którym S(2;−4) r=1 ad.2 5y = −3x−7

	3		7
y = −		x −
	5		5

(m+10)y = m²x+2

	1
dla m= −10 masz równanie 100x+2 = 0 czyli x = −
	50

a to jest prosta || do OY i na pewno nie jest prostopadła do danek dla m≠ −10 możesz podzielić przez m+10

	m2		2
y =		+
	m+10		m+10

	3		m2
−		*		= −1 /*(−5)(m+10)
	5		m+10

3m² = 5(m+10) 3m² − 5m − 10 = 0 rozwiąż i podstaw do podanego równania prostej 4.

	log122		a
log62 =		=		=
	log126		12   log12   2

a		a
	=
log1212−log122		1−a

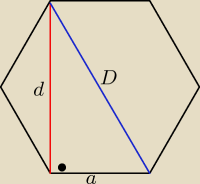
Basia: D = 2a d²+a²=(2a)² d² = 3a² d = a√3 a√3=3√3 a = 3

	a2√3
P = 6*
	4

dokończ

Basia: Bardzo Dziękuje!