Matura
bezendu:
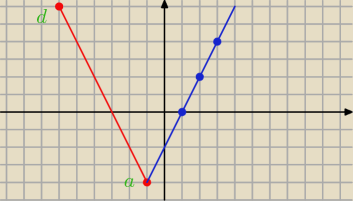
Oblicz pole i obwód rombu ABCD wiedząc, że przekątna AC jest zawarta w prostej o równaniu
y=2x−2(ta niebieska linia) oraz A=(−1,−4) D=(−6,6)
|AD|=
√(−6+1)2+(6+4)2=
√125=5
√5
Obw=4*5
√5=20
√5
Jak policzyć pole

( wskazówka nie rozwiązanie)

26 maj 15:44
Nienor:
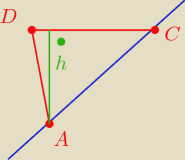
Potrzebne ci jest h, czyli odległość od prostej zawierającej DC. Wiesz, że C=(x,2x−2) i że
|DC|=|DA|
26 maj 16:00
bezendu:
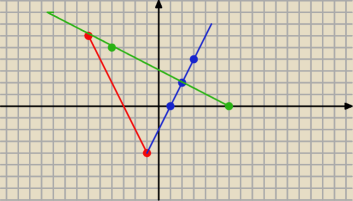
ja próbowałem zrobić tak że wyznaczyć prostą prostopadłą czyli drugą przekątną przechodzącą
przez punkt D
zielona to druga przekątna
26 maj 16:10
bezendu: czerwona prosta ma postać y=2x−2
| | 1 | |
zielona prostopadła do niej y=− |
| x+3 |
| | 2 | |
jeśli chcę wyznaczyć punkt przecięcia się tych prostych to mogę to przyrównać
2,5x=5
x=2
y=2
P=(2,2) ?
26 maj 16:16
bezendu:
P=(2,2)
A=(−1,−4)
D=(−6,6)
|AP|=
√(2+1)2+(−4−2)2=3
√5
|DP|=
√(2+6)2+(2−6)2=4
√5
|BD|=2*|DP|=2*4
√5=8
√5
|AC|=2*|AP|=2*3
√5=6
√5
| | |AC|*|DB| | | 8√5*6√5 | |
P= |
| = |
| =120 |
| | 2 | | 2 | |
ok ?
26 maj 16:31
bezendu: 
26 maj 17:57
Basia:
| | 1 | |
P = 4* |
| *AP*DP = 2AP*DP = 2*3√5*4√5 = 24*5 = 120 |
| | 2 | |
zgadza się
26 maj 18:05
bezendu: A jak zrobić to zadanie innym sposobem

26 maj 18:31
Basia: można inaczej, ale rachunki będą paskudne więc nie wiem czy warto
wyznaczasz B szukając punktów wspólnych y=2x−2
i okręgu o środku w A i r=5
√5
26 maj 18:49
bezendu: ok spróbuje to na brudno zrobić

26 maj 18:51
Basia: oczywiście P = |d(AB
⇒;AD
⇒)|
to nie trójkąt

26 maj 19:12
bezendu: właśnie coś mi nie wychodziło

ale już jest rozwiązanie

dziękuję
26 maj 19:15
 Oblicz pole i obwód rombu ABCD wiedząc, że przekątna AC jest zawarta w prostej o równaniu
y=2x−2(ta niebieska linia) oraz A=(−1,−4) D=(−6,6)
|AD|=√(−6+1)2+(6+4)2=√125=5√5
Obw=4*5√5=20√5
Jak policzyć pole
Oblicz pole i obwód rombu ABCD wiedząc, że przekątna AC jest zawarta w prostej o równaniu
y=2x−2(ta niebieska linia) oraz A=(−1,−4) D=(−6,6)
|AD|=√(−6+1)2+(6+4)2=√125=5√5
Obw=4*5√5=20√5
Jak policzyć pole  ( wskazówka nie rozwiązanie)
( wskazówka nie rozwiązanie) 
 Potrzebne ci jest h, czyli odległość od prostej zawierającej DC. Wiesz, że C=(x,2x−2) i że
|DC|=|DA|
Potrzebne ci jest h, czyli odległość od prostej zawierającej DC. Wiesz, że C=(x,2x−2) i że
|DC|=|DA|
 ja próbowałem zrobić tak że wyznaczyć prostą prostopadłą czyli drugą przekątną przechodzącą
przez punkt D
zielona to druga przekątna
ja próbowałem zrobić tak że wyznaczyć prostą prostopadłą czyli drugą przekątną przechodzącą
przez punkt D
zielona to druga przekątna




 ale już jest rozwiązanie
ale już jest rozwiązanie  dziękuję
dziękuję