dziękuję
:): Na ile sposobów można umieścić 16 jednakowych piłek w czterech różnych pudełkach?
a) N(19, 3)
b) (16 + 3)!
c) 16!
d) 4! 16!
26 maj 13:56
:): proszę o pomoc

26 maj 14:35
Basia: na poziomie szkoły średniej czy matematyki dyskretnej na studiach ?
26 maj 14:46
:): matematyki dyskretnej na studiach

26 maj 14:50
Basia: pamiętam tylko tyle, że jeżeli żadne pudełko nie może być puste to będą to liczby Stirlinga
drugiego rodzaju i to byłoby {16 nad 4}, ale tu nie ma takiej odpowiedzi więc zapewne nie jest
to takie proste; Mila pomoże jak się pojawi
26 maj 15:17
26 maj 15:49
Janek191:
N = 416 = 4 294 967 296
26 maj 17:19
Basia:
Janek191 zajrzyj do treści zadania i mojego pytania 14:46
tak jak napisałeś jest ⇔ i piłki, i pudełka są rozróżnialne (tak robicie w szkole)
tutaj piłki są nierozróżnialne i to jest zupełnie inny problem
26 maj 17:22
PW: Wkładanie 16 piłek do czterech różnych (rozróżnialnych) pudełek to inaczej przedstawienie
liczby 16 w postaci sumy czterech liczb naturalnych (z uwzględnieniem kolejności składników),
z których co najmniej jedna nie jest zerem. Mówiąc inaczej: liczymy wszystkie 4−elementowe
ciągi liczb naturalnych, w których suma elemenów jest równa 16. Gdyby wszystkie elementy były
dodatnie, to policzenie liczby takich ciągów nie sprawia trudności:
(1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1)=16.
Wstawiając w 3 miejscach "
," zamiast "
+" otrzymamy ciąg 4−elementowy o sumie 16, np.
1+1+1
,1+1+1+1
,1+1+1+1+1+1
,1+1+1
oznacza, że utworzyliśmy ciąg (3
,4
,6
,3).
Ponieważ jest
sposobów wyboru 3 spośród 15 znaków "
+", tyle jest możliwości rozłożenia 16 piłek do 4
pudełek przy założeniu, że żadne pudełko nie pozostanie puste. Takiego założenia w zadaniu nie
ma, więc trzeba uwzględnić również:
ciągów o 3 elementach dodatnich i jednym zerowym (pierwszy czynnik to liczba sposobów wyboru 3
miejsc spośród 4, a drugi − liczba sposobów utworzenia 3−elementowych ciągów o sumie 16 i
wyrazach dodatnich)
ciągów o 2 elementach dodatnich i dwóch zerowych oraz
ciągi o trzech wyrazach zerowych i jednym równym 16.
| | | |
Zsumowanie liczb (1), (2), (3) i (4) daje 969, co jak łatwo sprawdzić jest równe | . |
| | |
27 maj 22:28
Mila:
Zadanie jest równoważne z liczbą rozwiązań równania w zbiorze liczb nieujemnych całkowitych.
1)
x
1+x
2+x
3+x
4=16
2)
Liczba rozwiązań dodatnich : ( żadne pudełko nie jest puste)⇔ x
i∊N+
| | | |
= | nie ma dystraktora o takiej wartości. |
| | |
Zatem
odp. A
27 maj 22:43
PW: Ponieważ mój sposób był "metodą babci pod piecem" (babcia ma dużo czasu, to sobie powolutku
policzy):
| | | | | | | |
1• | + 4• | + 6• | + 4•{15}{0}, |
| | | | |
a
Mila podała gotowy wzór
wypada pokazać rozumowanie prowadzące wprost do tego wzoru.
Można pomyśleć tak:
Do 16 białych piłek umieszczonych w czwartym pojemniku dokładamy 3 czerwone, mieszamy piłki i
nie oglądając wyciągamy.
1. Wyciągane piłki wrzucamy do pojemnika nr 1 aż napotkamy piłkę czerwoną.
2. Dalej wyciągamy piłki i wrzucamy do pojemnika nr 2 aż napotkamy drugą piłkę czerwoną.
3. Dalej wyciągamy piłki i wrzucamy do pojemnika nr 3 aż napotkamy trzecią piłkę czerwoną.
4. W pojemniku nr 4 pozostają piłki, których nie wylosowaliśmy (w szczególnym przypadku może
ich nie być wcale).
W ten sposób wszystkie białe piłki zostały umieszczone w jednym, dwóch, trzech lub czterech
pojemnikach.
Liczby białych piłek w poszczególnych pojemnikach wahają się od 0 do 16, w zależności od tego,
w których losowaniach wypadały piłki czerwone.
Sposobów losowania 3 elementów spośród 19 jest
a więc na tyle sposobów można było rozmieścić 16 białych piłek w czterech pojemnikach.
Kto nie lubi czerwonych, może je wyrzucić − swoją rolę "przecinków" już spełniły.
Można tę liczbę zapisać w postaci
− widać wtedy liczbę piłek 16 i liczbę pojemników 4
Rozumowanie jest o tyle lepsze, że na jego podstawie odpowiadamy bez wątpliwości:
| | | |
n nierozróżnialnych elementów można rozmieścić w k pojemnikach na | sposobów. |
| | |
I w tym momencie
doznałem olśnienia − już wiem, dlaczego w pewnych szkołach są klasy,
które mają 6 godzin wf i 2 godziny matematyki. Wystarczy pobawić się piłkami, żeby pojąć
trudne problemy matematyczne, takie jak znalezienie liczby rozwiązań równania
x
1+x
2+x
3+...+x
n=k.
30 maj 01:26
Basia: Świetny sposób
PW.

30 maj 10:35
Mila: Pięknie !
Tylko zmiana:
x1+x2+...+xk=n
Niewiadomych tyle, ile pojemników.
30 maj 16:11
PW: Mila, dziękuję za poprawkę (przestawiłem n i k, winię za to późną godzinę).
Basiu, dziękuję za pochwałę, zawsze to miło, gdy fachowcy zauważą wysiłki

30 maj 18:47
Mila: 
30 maj 19:05
Aero: witam
Mógłby mi ktoś wytłumaczyć skąd się wziął wynik 3 w x1 + x2 + x3 + x4 + x5 = 3
19 wrz 20:58
Aero: w odniesieniu do wypowiedzi użytkowniczki mila
Rozwiązać równanie:
x1+x2+x3+x4+x5=4 w zbiorze liczb całkowitych nieujemnych
jest równoważne z problemem na ile sposobów możesz zapisać liczbę 4 w postaci sumy 5
składników naturalnych , z tym, że x1 nie może być równe 0.
W takim razie x1≥1 i mamy równanie:
x1+x2+x3+x4+x5=3
I tak sytuację :4=1+1+2+0+0
Można to obrazowo przedstawić, że masz 5 szuflad i do pierwszej szuflady włożono jedną kulę, do
drugiej 1 kulę do trzeciej 2 kule do czwartej i piątej nie włożono kul (0 kul).
Kule są nierozróżnialne (identyczne).
gdzie n=3, k=5⇔
19 wrz 21:02
Aero: tresc zadania
Oblicz, ile jest liczb 5−cyfrowych o sumie cyfr 4.
19 wrz 21:02
Mila:
Aero , jaką masz treść zadania, podane masz ograniczenie co x1?
19 wrz 21:11
Aero: ograniczenie jest takie,że pierwsza liczba nie może być 0
19 wrz 21:14
Aero: bardzo bym prosił o dokładne wytłumaczenie tego co tam zaszło ( nie boje sie tego powiedziec
wytłumaczenie jak dla idioty

) zaczynam dopiero uczyć się kombinatoryki a ten wzór wydaje
mi się bardzo przydatny,dlatego usiłuje go zrozumieć
19 wrz 21:17
Mila:
W takim razie dobrze.
Do pierwszej szuflady wrzuciłeś jedna kulę, to zostały 3
i masz równanie :
x
1+x
2+x
3+x
4+x
5=3 oraz pewność, że otrzymasz liczbę 4 cyfrową cokolwiek wpadnie ( lub nie)
do pierwszej szuflady
Liczba rozwiązań w zbiorze liczb całkowitych nieujemnych:
Można to zresztą na piechotę policzyć, ale zawsze można coś pominąć.
13 000 4 liczby
31 000 4
12 100 12
21 100 6
11 200 4
22 000 4
40 000 1
=============
35
19 wrz 21:28
Aero: Myślę,że zrozumiałem,nawet jeśli nie to na piechotę dam rade.
Dziękuje za poświęcony czas . Dobranoc

19 wrz 21:37
Mila:
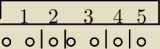
Ten wzór to kombinacje z powtórzeniami.
A={a,b,c} masz dany zbiór 3 elementów .
Liczba kombinacji 2−elementowych z powtórzeniami zbioru 4−elementowego A = {a, b, c}
{a,a}, {b,b},{c,c}, {a,b},{a,c},{b,c}
Ważne abyś wiedział w jakich sytuacjach to zastosować.
Dotyczy rozmieszczenia n jednakowych obiektów( jednakowe kule) w k rozróżnialnych kategoriach
(różne szuflady).
Inaczej można rozwiązać zadanie ile jest liczb 5− cyfrowych o sumie cyfr 7 i żadna nie jest
zerem.
x
1+x
2+x
3+x
4+x
5=7
Masz 7 jednakowych kul
Aby rozmieścić je tak, aby w każdej szufladzie znajdowała co najmniej jedna kula
trzeba ustawić 4 przegrody.
Na te przegrody masz do wyboru 6 miejsc
tu masz zwykłe kombinacje.
Ustaliłeś ile rozwiązań ma równanie w zbiorze liczb całkowitych dodatnich.
=================================
Możesz postąpić jak poprzednio
x
1+x
2+x
3+x
4+x
5=7 gzie x
i≥1 i x
i∊N
7−5=2 wrzucamy po jednej kuli do każdej szuflady
Teraz szukamy liczby rozwiązan równania
x
1+x
2+x
3+x
4+x
5=2
w zbiorze C∪{0}
19 wrz 21:58
Yumegari: Na ile sposobów można umieścić w 3 szufladach 7 bluzek?
10 lut 16:24





 ) zaczynam dopiero uczyć się kombinatoryki a ten wzór wydaje
mi się bardzo przydatny,dlatego usiłuje go zrozumieć
) zaczynam dopiero uczyć się kombinatoryki a ten wzór wydaje
mi się bardzo przydatny,dlatego usiłuje go zrozumieć

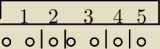 Ten wzór to kombinacje z powtórzeniami.
A={a,b,c} masz dany zbiór 3 elementów .
Liczba kombinacji 2−elementowych z powtórzeniami zbioru 4−elementowego A = {a, b, c}
{a,a}, {b,b},{c,c}, {a,b},{a,c},{b,c}
Ten wzór to kombinacje z powtórzeniami.
A={a,b,c} masz dany zbiór 3 elementów .
Liczba kombinacji 2−elementowych z powtórzeniami zbioru 4−elementowego A = {a, b, c}
{a,a}, {b,b},{c,c}, {a,b},{a,c},{b,c}