Trójkąty Piotruś: 1. W trójkącie prostokątnym ABC, w którym kąt C=90 poprowadzono odcinek CD w taki sposób, że D∊AB oraz kąt BCD=2ACD. Wykaż, że jeżeli pola trójkątów ADC i BCD są równe, to kąty ostre trójkąta ABC mają miarę 30 i 60. 2. W trójkącie ABC poprowadzono dwusieczną z pkt C, która przecięła bok AB w pkt D. Wiedząc, że AC=12, BC=4 oraz pole trójkąta ADC jest o 6√3 cm² większe od pola trójkąta DBC, oczlicz pole trójkąta ABC. Proszę o pomoc

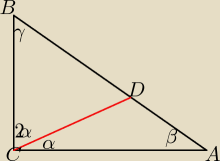
Basia: α+2α=90 3α=90 α=30 2*P_ADC = AC*CD*sinα 2*P_BDC = BC*CD*sin(2α) P_ADC = P_BDC tp AC*CD*sinα = BC*CD*sin(2α) / :CD AC*sinα = BC*2sinα*cosα / :sinα (można bo sinα≠0) AC = 2BC*cosα

	AC
cos30 =
	2BC

√3		AC
	=		/*2
2		2BC

	AC
√3 =
	BC

AC = √3*BC

	BC		BC		1		√3
tgβ =		=		=		=
	AC		√3BC		√3		3

stąd β = 30 i γ=90−30 = 60

Piotruś: Dzięki

Piotruś: Ktoś umie zad. 2?

Basia: na pewno dobra treść ? bo straszne rzeczy mi wychodzą

Piotruś: Tak, treść jest dobra.

Basia:

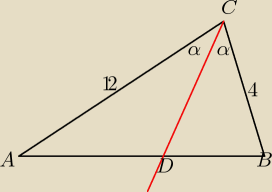
	1
PDBC =		*4*CD*sinα = 2*CD*sinα
	2

	1
PDAC =		*12*CD*sinα = 6*CD*sinα
	2

stąd mamy

PDAC		6*CD*sinα
	=		= 3
PDBC		2*CD*sinα

P_DAC = 3*P_DBC z treści P_DAC = P_DBC+6√3 3*P_DBC = P_DBC+6√3 2*P{DBC} = 6√3 P_DBC = 3√3 P_DAC = 3*3√3 = 9√3 P_ABC = 3√3+9√3 = 12√3