zadania Saizou : z powodu wielkiej nudy jaka nastała w dniu dzisiejszym poprosiłbym o jakieś ciekawe zadanie, poziom LO z klasy I i II (czyli całe LO bez kombinatoryki, prawdopodobieństwa, funkcji wymiernej), a myślę że resztę dam rade

k20: dlaczego bez wymiernej?

Saizou : bo f. wymierna to materiał z 3 klasy Lo, ale podstawy znam

bezendu: http://users.v-lo.krakow.pl/~climek/ebooki/pompe.pdf na nudę

Mateusz: a geometria moze byc?

Saizou : może być

Mateusz: No to na wieczorny deserek: Wykaż że jeden z kątów trójkąta o bokach: a=m²−2m b=m²−1, c=m²−m+1 jest równy 60^o

Basiek: Oj, korzystaj z weekendu! Naprawdę.

Mateusz: Ma korzystać z nudy ?

Saizou : Basiek, a czemu nie jesteś kolorowa właśnie korzystam z weekendu z matematyką , a tak na serio jutro muszę dość wcześnie wstać i nie mogę dzisiaj balować

Basiek: Możemy się zamienić! Nuda jest.... cudowna. Naprawdę.

Basiek: Zakolorowanie wymaga zalogowania. A ja jestem leniwa. Wyjątkowo leniwa.

Mateusz: Błoga nuda w sumie masz racje

Saizou : Mateusz można to zrobić z tw. cosinusów, tylko trzeba określić, który bok jest najdłuższy. Najdłuższym bokiem będzie bok b=m²−1 i trzeba dać założenie że m>2 dobrze myślę?

Mila: https://matematykaszkolna.pl/forum/204565.html Za chwilę inne zadanie godne przyszłego maturzysty.

Saizou : w sumie to dla każdego z kątów trzeba zastosować twierdzenie

Mateusz: a=m²−2m b=m²−1 c=m²−m+1 taK dobrze myslisz

Saizou : Mila w tym zdaniu wystarczy pokazać że ta suma jest liczbą całkowitą

Saizou : bo podzielność mamy bo 2005=5*401

I've done the Harlem Shake: Siema Mateusz, tu tabletowy Theosh Jak możesz to linkuj 204622

Krzysiek : Np. Wykonac dzialanie :

x		1
	*4√(1+2x+x2)(x+1)(x2−1) −4√x5(1−x−1)+		x3*4√x−3−x−4
2		2

Zadnie nr 2 . Rozwiaz rownanie

√x2−16		7
	+√x+3=
√x−3		√x−3

Na razie te dwa.

Saizou : na razie Stop z zdaniami, bo ich nie ogarnę

Mila: 1) Wielomian dla Saizou Dla jakich parametrów p i q wielomian: W(x)=64x³+48x²+px+q ma pierwiastek trzykrotny? 2) Równanie Rozwiąż: (x²−x+1)³−6(x²−x)²−2*(x²−x+2)=0

Mila: Wyjaśnij dokładnie, dlaczego całkowita suma dzieli się przez 2005.

Saizou : Mila jeśli ma pierwiastek 3−krotny to idzie go zwinąć do wzorku (a±b)³ Mateusz na pewno to nie jest to kąt między bokami a,c

Mateusz: hmm a z jakiej funkcji trygonometrycznej skorzystasz? Czesc Harlen czy jak ci tam odpowiedziałem ci juz

Saizou : może gdzieś się rachunkowo kopnąłem, przeliczę jeszcze raz

Saizou : W(x)=64x³+48x²+px+q a³=64x³→a=4x 3a²b=48x² 3*16x²*b=48x² b=1 W(x)=(4x+1)³=64x³+48x²+12x+1 p=12 q=1

Mila:

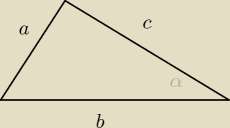
Saizou : a=m²−2m b=m²−1 c=m²−m+1 z tw. cosinusów c²=a²+b²−2ab*cosα α=x dla ułatwienia zapisu (m²−m+1)²=(m²−2m)²+(m²−1)²−2(m²−2m)(m²−1)cosx (m²−m+1)²−(m²−1)²=(m²−2m)²−2(m²−2m)(m²−1)cosx (−m+2)(2m²−m)=(m²−2m)²−2(m²−2m)(m²−1)cosx −2m³+5m²−2m=m⁴−4m³+4m²−2cosx(m⁴−2m³−m²+2m) −m⁴+2m³+m²−2m=−2cosx(m⁴−2m³−m²+2m) 1=2cosx

	1
cosx=		→x=60
	2

ZKS: Mi się też nudzi więc rozwiąże równanie które podała Mila. (x² − x + 1)³ − 6(x² − x)² − 2 * (x² − x + 2) = 0 (x² − x + 1)³ − 6(x² − x + 1 − 1)² − 2(x² − x + 1 + 1) = 0 (x² − x + 1)³ − 6(x² − x + 1)² + 12(x² − x + 1) − 6 − 2(x² − x + 1) − 2 = 0 x² − x + 1 = t t³ − 6t² + 10t − 8 = 0 t³ − 64 − 6t² + 10t + 56 = 0 (t − 4)(t² + 4t + 16) − (t − 4)(6t + 14) = 0 (t − 4)(t² − 2t + 2) = 0 x² − x + 1 = 4 x² − x − 3 = 0 Δ = 1 + 12 √Δ = √13

	1 ± √13
x =		.
	2

Mila: Albo x²−x=t (t+1)³−6t²−2(t+2)=0 Wynik jak u ZKS

Mateusz:

Nienor: Rozwiążę sobie Krzyśka zad 1

x		1
	4√(1+2x+x2)(x+1)(x2−1) −4√x5(1−x−1)+		x3*4√x−3−x−4=
2		2

x		x−1		1		x−1
	4√(x+1)4(x−1)−4√x5		+		x34√		=
2		x		2		x4

x(x+1)		1		4√x−1		4√x−1
	4√x−1−4√x−1+		x4√x−1=		(x2+x−2+x)=		(x2+2x−2)
2		2		2		2

I x−1≥0 i x≥0 i x+1≥0 zad 2

√x2−16		7
	+√x+3=
√x−3		√x−3

Z: x−3>0 ⇒ x>3 x+3≥0 ⇒ x≥−3 (x−4)(x+4)≥0 ⇒ x∊(−∞,−4]∪[4,+∞) x∊[4,+∞) √x²−16+√x²−9=7 x²−9=49−14√x²−16+x²−16 42=14√x²−16 3=√x²−16 9=x²−16 0=x²−15 x=5 ∨ x=−5∉[4,+∞) Odp. x=5