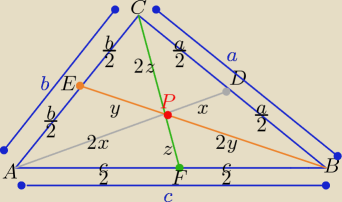
 |AD|=Sa =3x, |BE|=Sb=3y, |CF|=Sc=3z
Z nierówności trójkąta:
|AD|=Sa =3x, |BE|=Sb=3y, |CF|=Sc=3z
Z nierówności trójkąta:
| b | ||
2x+2y>c 2x+y> | ||
| 2 |
| c | ||
2x+2z>b 2y+z> | ||
| 2 |
| a | ||
2y+2z>a 2z+x> | ||
| 2 |
| 3 | a+b+c | |||
4x+4y+4z> a+b+c /* | 3x+3y+3z> | |||
| 4 | 2 |
| 3(a+b+c) | a+b+c | |||
3x+3y+3z> | Sa+Sb+Sc> | < a+b+c | ||
| 4 | 2 |
| 3(a+b+c) | ||
Sa+Sb+Sc> | ||
| 4 |
| 3(a+b+c) | ||
zatem | < Sa+Sb+Sc < a+b+c | |
| 4 |


| 1 | ||
A jasne jest dla Ciebie to,że | <1 | |
| 2 |
| a+b+c | ||
zatem | < a+b+c | |
| 2 |


 2)
Sa+Sb+Sc < a+b+c
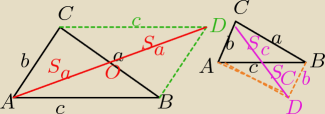
Patrz rysunek:
Uzupełniam ΔABC do równoległoboku ABDC, z własności równoległoboku
i własności odległości mamy:
2Sa<b+c w ΔADC
Podobnie:
2Sc<a+b
Analogicznie mamy:
2Sb<a+c
stąd:
2Sa+2Sb+2Sc<b+c+a+b+a+c⇔2Sa+2Sb+2Sc<2(a+b+c)⇔
Sa+Sb+Sc<a+b+c
2)
Sa+Sb+Sc < a+b+c
Patrz rysunek:
Uzupełniam ΔABC do równoległoboku ABDC, z własności równoległoboku
i własności odległości mamy:
2Sa<b+c w ΔADC
Podobnie:
2Sc<a+b
Analogicznie mamy:
2Sb<a+c
stąd:
2Sa+2Sb+2Sc<b+c+a+b+a+c⇔2Sa+2Sb+2Sc<2(a+b+c)⇔
Sa+Sb+Sc<a+b+c
