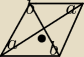
Oblicz pole tego rombu oraz miary jego kątów. wajdzik: Bok rombu ma długość √5,a krótsza przekątna 2√2. Oblicz pole tego rombu oraz miary jego kątów.

	√2		√5		√10
sinα=		*		=
	√5		√5		5

sinα≈0,63 sinα=39(stopni) 2sinα=78(stopni) cosβ≈0,63 cosβ=51(stopni) 2cosβ=102(stopnie) P=a²sinα=5*0,63=3,15[j²] Zgadza się?

wajdzik:

wajdzik:

Krzysiek : . rowniez kat 2β mogles obliczyc z zaleznosci ze 2β=180−2α natomiast przy obliczeniu pola powinno byc P=a²*2sin alfa bo kat miedzy ramionami rombu na rysunku jest 2 alfa .

Krzysiek : U Ciebie na rysunku kat α to kat pomiedzy bobiem a dluzsza przekatna a nie pomiedzy dwoma bokami

krystek: lub z tw cosinusów d²=a²+a²−2a*acosα

Eta: 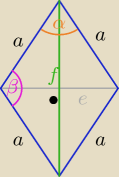f²+e²= 4a² ⇒ f²=4*5−8 ⇒ f= 2√3

	e*f
P=		= 2√6 i P=a2*sinα
	2

	2√6
to sinα=		⇒ α≈ ........ odczytaj z tablic, β= 180o −α=..........
	5

wajdzik: α=78(stopni) β=102(stopnie)