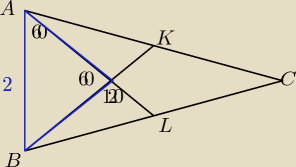
pole trójkąta spirner: Podstawą trójkąta ABC jest bok AB. Środkowe AL i BK przecinają się w punkcie S pod kątem 60stopni. Wiadomo, że pole trójkąta ABS jest równe √3. a) Oblicz długość boków trójkąta ABC. b) Czy kąt ACB jest równy 30 stopni? Uzasadnij obliczyłem, że bok |AB| = 2

	√3
oraz pole P BSL=P ASK =
	2

|SK|=|SL|=1 |AS|=|SB|=2

	3√3
P ABL = P AKB =
	2

trójkąt ASB jest równoboczny tylko nie wiem jak obliczyć pozostałe boki

spirner: ma ktoś pomysł

spirner: naprawdę nikt ni ma przynajmniej pomysłu ?

Eta: Czy trójkąt ABC jest równoramienny? ( bo nie napisałeś tego

spirner: Trójkąt abc jest równoramienny

Basia: to drugie 60^o przy wierzchołku A niebieskiego trójkąta było podane ?

Basia: jeżeli tak to teraz masz: AB = AS = BS = 2 SL=SK = 1 (bo S dzieli środkowe w stosunku 1:2) x=AK = BL możesz wyliczyć z tw.cosinusów

	1
x2 = 22+12−2*2*1*cos120 = 4+1+4*		= 7
	2

x = √7 AC = BC = 2√7 AB² = AC²+BC²−2*AB*AC*cos(∡ACB) 4 = 28+28−2*28*cos(∡ACB) 56*cos(∡ACB) = 56−4

	52		26		13		√3
cos(∡ACB) =		=		=		≠
	56		28		14		2

zatem |cos(∡ACB)| ≠ 30^o

spirner: wielkie dzieki