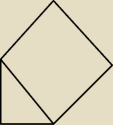
 Na przeciwprostokątnej AB trójkąta ABC o kątach ostrych α i β zbudowano kwadrat ADEB. Stosunek
pola kwadratu do pola trójkąta wynosi 5:1.
Oblicz wartość wyrażenia tg2α +tg2β
Na przeciwprostokątnej AB trójkąta ABC o kątach ostrych α i β zbudowano kwadrat ADEB. Stosunek
pola kwadratu do pola trójkąta wynosi 5:1.
Oblicz wartość wyrażenia tg2α +tg2β
| 1 | ||
tg2α + tg2β = tg2α + ctg2α = | ||
| sin2αcos2α |
| a | ||
sinα = | ||
| c |
| b | ||
cosα = | ||
| c |
| Pkw | c2 | 2c2 | 2 | ||||||||||
= 5 ⇒ | = | = | = 5 ⇒ | ||||||||||
| Ptr |
| c2 * sinαcosα | sinαcosα |
| 1 | 5 | 25 | |||
= ( | )2 = | ||||
| sin2αcos2α | 2 | 4 |
| 25 | ||
tg2α + tg2β = | ||
| 4 |
 inaczej , a
więc z warunków zadania przy standardowych
oznaczeniach :
inaczej , a
więc z warunków zadania przy standardowych
oznaczeniach :
| P□ | 5k | c2 | 2(a2+b2) | ||||
= | ⇔ | = 5 ⇔ | = 5 ⇔ | ||||
| PΔ | k | 12ab | ab |
| a | b | |||
⇔ 2( | + | )= 5 ⇔ 2(tgα+tgβ)= 5 /2 ⇔ 4(tg2α+2tgαtgβ+tg2β)= 25 /:4 ⇔ | ||
| b | a |
| 25 | 25 | 8 | ||||
⇔ tg2α+2*1+tg2β= | ⇔ tg2α+tg2β= | − | ⇔ | |||
| 4 | 4 | 4 |
| 17 | ||
⇔ tg2α+tg2β= | − szukana suma kwadratów tangensów . ...  | |
| 4 |
| a | b | |||
zauważ, że tgαtgβ= tgαtg(90o−α)= tgαctgα= 1, lub inaczej tgαtgβ= | * | = 1. | ||
| b | a |

| sin2α | cos2α | sin4α + cos4α | ||||
tg2α + ctg2α = | + | = | = | |||
| cos2α | sin2α | sin2αcos2α |
| 1 − 2sin2cos2α | 1 | ||
= | − 2 | ||
| sin2αcos2α | sin2αcos2α |