Całka manuel:

	⎧	c dla 1≤|x|≤2, 1≤|y|≤2
f(x,y) =	⎨
	⎩	0 dla pozostałych (x,y)

	1
Wyliczyć parametr c, ma wyjść
	12

Obliczyłem, ale wyszedł mi zły wynik, tak zrobiłem: ∫₁²∫₁² cdxdy = c∫₁²(∫₁²dy)dx = ∫₁² cdx = c = 1

manuel:

manuel:

manuel:

manuel:

manuel:

manuel:

manuel:

manuel:

manuel:

manuel:

Godzio: Ale co masz wyliczyć ?

manuel: wyliczyć parametr c poprzez ∫_∞^∞∫_∞^∞ f(x,y)dxdy = 1

manuel:

Godzio:

	1
A możesz dokładnie podać skąd to masz ? Z tymi danymi c na pewno nie wyjdzie
	12

manuel: Mogę coś podać dokładnie, tylko pytanie, co?

	1
Zadanie pochodzi z książki Plucińskich, tam w odpowiedziach widnieje odpowiedź		.
	12

Nie wiem, czy tam jest błąd. A nie przypadkiem chodzi o |x| i |y|? Może o to chodzi?

manuel: ∫_∞^∞∫_∞^∞f(x,y)dxdy = = ∫∫ cdxdy = ..... −−−−− tutaj nie wiem, jaka to będzie całka

Godzio: 1 ≤ |x| ≤ 2 ⇔ 1 ≤ x ≤ 2 lub −1 ≥ x ≥ − 2 1 ≤ |y| ≤ 2 ⇔ 1 ≤ y ≤ 2 lub −1 ≥ y ≥ − 2

	1
Więc nawet jak się porobi wszystkie możliwe kombinacje to i tak wychodzi c =
	4

manuel: Jeśli tak wychodzi, to możesz napisać, jak obliczyłeś?

manuel: będą tutaj 4 całki?

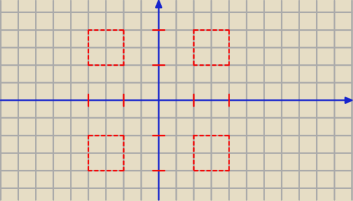
Godzio: ∫∫_Dcdxdy gdzie D = { (x,y): 1 ≤ |x| ≤ 2 i 1 ≤ |y| ≤ 2 } czyli ∫∫_Dcdxdy = c * (∫₁²∫₁²dxdy + ∫₋₂⁻¹∫₋₂⁻¹dxdy + 2∫₋₂⁻¹₁²dxdy) = 1

	1
c * (1 + 1 + 2) = 1 ⇒ c =
	4

Ale głowy nie dam, że tak jest

manuel: Okej, może jednak jest błąd w książce Dziękuję bardzo za pomoc