całka potrójna ad: Korzystając z całki potrojnej oblicz objętość obszaru ograniczonego powierzchniami: x²+y²=2, y=√x; y=0; z=0 z=15x

Vizer: Musisz spróbować narysować te krzywe w układzie współrzędnych: 1) x² + y² = 2 − to walec 2) y = √x − to również walec tylko chyba fachowo nazywa się parabolicznym 3) i 4) z = 0 i z= 15x − to płaszczyzny które będą ograniczały nasz obszar

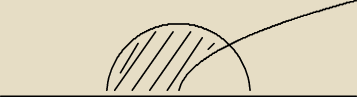
ad: narysowałem wcześniej, wg mnie opis powinien być taki ale niekoniecznie mi to wychodzi... w postaci jawnej: 0 < y < √2 √2−x² < x < √x 0 < z < 15x nie wiem za bardzo jak powinno to wyglądać dla wsp walcowych...

F1: x² + y² = 2 Jaki walec? OKRĄG nieuku.. A jak już rozpatrujemy układ XYZ to kula

ad: Vizer; Krzysiek, pomóżcie!

ad: no chyba chciałeś zablysnąć i cos Ci nie poszlo F1... na płaszczyznie xy jest to rownanie okregu, a przesuwajac to wzdluz osi z otrzymujemy walec. Dla przypomnienia rownanie kuli to x²+y+2+z²=R²

ad: oczywiscie tam y² a nie y+2

Vizer: F1 zastanów się jeszcze raz zanim coś napiszesz i kogoś obrazisz. Kula odpada już na starcie bo ma "wnętrze", jak coś to sfera, ale też nie w tym zadaniu. Wzór na sferę to (x − a)² + (y − b)² + (z − c)² = r², tutaj nie ma to zastosowania. ad jeśli nikt inny nie napisze szybciej to zaraz Ci pomogę tylko sam muszę sobie przypomnieć jak to się liczyło

F1: Bardzo przepraszam, jestem po maturze Te rzeczy będę robić dopiero na studiach bo idę na matematykę na UŁ Pozdrawiam i proszę pamiętać o GP Monaco niedziela godz. 14 Dziękuję za napisanie równania kuli i sfery gdyż bardzo mi się to przyda

ad: nie jestem pewien, ale dla wsp walcowych ten opis powinien tak wygladac, 0 < r < √2 π/4 < φ < π 0 < z < 15 cosφ

ad: poprawka, 0<z<15rcosφ

ad: albo i nie, wolfram pokazuje mi wynik −10, trzeba byloby wziąć wartość bezwzględną z tego. Mimo wszystko nie zgadza mi się to z odpowiedziami w których mam wynik 11

ad: pomoze ktos?

Vizer: Moje granice to :

	π
0 ≤ φ ≤
	4

0 ≤ r ≤ √2 0 ≤ z ≤ 15rcosφ i wychodzi mi 10, nie wiem czemu ma być 11.

wtf: mógłbyś wyjaśnić czemu φ zawiera się w granicach [0;π/4]?

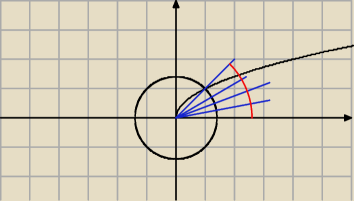
Vizer: Na rysunku widać półproste, które wychodzą z środka układu współrzędnych i "przebijają" nasz okrąg, półprosta, która przecina się w jednym punkcie z z dwoma krzywymi, wyznacza nam kąt φ,

	π
który wynosi		, gdyż ta półprosta jest częścią prostej o równaniu y = x.
	4

Krzysiek: To co Vizer napisałeś to nie będzie cała objętość tej bryły, został 'kawałek' pominięty na płaszczyźnie XY dla φ≥π/4

Vizer: Hmm faktycznie, zrobiłem to dla przykładu gdybyśmy mieli zamiast y = √x, to y = x. Możesz napisać jakby to wyglądało?

Vizer: Można dodać do tej objętości całkę : ∫¹₀dx ∫^√x_xdy ∫^15x₀dz Tylko teraz czy można policzyć tą objętość za jednym zamachem?

Krzysiek: jak już korzystamy ze współrzędnych biegunowych to ten kawałek policzymy tak: http://www.wolframalpha.com/input/?i=integrate_%28pi%2F4%29%5E%28pi%2F2%29+%28integrate_%280%29%5E%28cos%28phi%29%2Fsin%5E2%28phi%29%29+%28integrate_%280%29%5E%2815rcos%28phi%29%29+rdz%29dr%29d%28phi%29

Krzysiek: A to co napisałeś to nie jest tylko ten brakujący kawałek więc objętość będzie za duża.

Vizer: Hmm wyszło mi z tego 1

Vizer: http://www.wolframalpha.com/input/?i=int%5E1_0%28int_x%5E%28sqrtx%29%28int%5E%2815x%29_0+1dz%29dy%29dx%29

Krzysiek: tak dobrze napisałeś źle popatrzyłem (myślałem że napisałeś granice całkowania dla y to 0 i √x )

Vizer: Widzę, że chyba nie ma sposobu na załatwienie tego jedną całką, chyba że jakoś po zmianie granicy całkowania. Zaraz spróbuję.

Krzysiek: http://www.wolframalpha.com/input/?t=crmtb01&f=ob&i=integrate_(0)%5E(1)(integrate_(y%5E2)%5E(sqrt(2-y%5E2))(integrate_(0)%5E(15x)dz)dx)dy

Vizer: Już też tak samo policzyłem Dzięki za skorygowanie tego powyższego błędu

Krzysiek: Bez wolframa nie chciało by mi się do tego zadania zabierać

Kamilek: odpowiedż do zadania to 12 pierwiastek 4 st z 2, a przedzuały całkowania to 0<=x<=√2 0<=y<=√x, 0<=z<=15x