 Witam mam problem z kilkoma zadaniami. Nie radzę sobie kompletnie, mam wątpliwości czy dobrze
to obliczyłem bo podkładałem dane pod inne obliczenia. Z niektórymi zadaniami w ogóle sobie
nie radzę i nie jestem w stanie się połapać co i jak. Dodam że nigdy nie miałem z nimi
styczności.
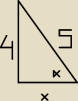
Zad1 Deska o długości 5m oparta jest o ścianę na wysokości 4m. Ile wynosi tangens kąta, pod
jakim jest nachylona do poziomu ta deska ?
tg α = 4cmx
Obliczam "x" z twierdzenia Pitagorasa
42 + x2 = 52
x2 = 25 − 16
x2 = 9
x = √9
x = 3m
tg α = 43
Z tabelki funkcji trygonometrycznych kątów ostrych odczytuję, że α ≈ 35*
Zad2 Dla jakich argumentów funkcja k (x) = x2 − 2x + 5 jest rosnąca ?
k(x) = x2 − 2x + 5
X2 − 2x + 5 > 0
Δ = (−2)2 − 4 * 1 * 5 = 4 − 4 * 1 * 5 = 4 − 4 * 5 = 4 − 20 = −16 < 0
ϰ ∊ ℛ co to w ogóle jest i czy dobrze to zapisałem ? bo podłapałem z innego przykładu
Zad 3* Jaki wzór ma funkcja liniowa, której wykres przechodzi przez punkt A = (12 , 2) i
jest równoległy do wykresu funkcji y = − 12 x +1
Zad 4* Znajdź wzór funkcji, której wykresem jest parabola o wierzchołku W = (7,6) przechodząca
przez punkt P = (1,2)
Zad 5* Znajdź zbiór rozwiązań nierówności x2 − x − 12 ≥ 0
* Za te zadania kompletnie nie wiem jak się zabrać, próbowałem podstawiać pod różne inne
przykładowe ale nic z tego nie wychodzi.
Proszę o pomoc mądrej główki która tak jak ja lubi pomagać innym.
Witam mam problem z kilkoma zadaniami. Nie radzę sobie kompletnie, mam wątpliwości czy dobrze
to obliczyłem bo podkładałem dane pod inne obliczenia. Z niektórymi zadaniami w ogóle sobie
nie radzę i nie jestem w stanie się połapać co i jak. Dodam że nigdy nie miałem z nimi
styczności.
Zad1 Deska o długości 5m oparta jest o ścianę na wysokości 4m. Ile wynosi tangens kąta, pod
jakim jest nachylona do poziomu ta deska ?
tg α = 4cmx
Obliczam "x" z twierdzenia Pitagorasa
42 + x2 = 52
x2 = 25 − 16
x2 = 9
x = √9
x = 3m
tg α = 43
Z tabelki funkcji trygonometrycznych kątów ostrych odczytuję, że α ≈ 35*
Zad2 Dla jakich argumentów funkcja k (x) = x2 − 2x + 5 jest rosnąca ?
k(x) = x2 − 2x + 5
X2 − 2x + 5 > 0
Δ = (−2)2 − 4 * 1 * 5 = 4 − 4 * 1 * 5 = 4 − 4 * 5 = 4 − 20 = −16 < 0
ϰ ∊ ℛ co to w ogóle jest i czy dobrze to zapisałem ? bo podłapałem z innego przykładu
Zad 3* Jaki wzór ma funkcja liniowa, której wykres przechodzi przez punkt A = (12 , 2) i
jest równoległy do wykresu funkcji y = − 12 x +1
Zad 4* Znajdź wzór funkcji, której wykresem jest parabola o wierzchołku W = (7,6) przechodząca
przez punkt P = (1,2)
Zad 5* Znajdź zbiór rozwiązań nierówności x2 − x − 12 ≥ 0
* Za te zadania kompletnie nie wiem jak się zabrać, próbowałem podstawiać pod różne inne
przykładowe ale nic z tego nie wychodzi.
Proszę o pomoc mądrej główki która tak jak ja lubi pomagać innym.
| −b | 2 | |||
xw= | = | =1 | ||
| 2a | 2 |
| b | 2 | |||
wzorek na współrzędna x wierzchołka to xw=− | czyli xw= | =1 | ||
| 2a | 2 |
| 1 | ||
przed x) sa takie same. więc wzorek tej drugie funkcji to y=− | x+b i wiemy, że przechodzi | |
| 2 |
| 1 | 1 | |||
2=− | * | +b | ||
| 2 | 2 |
| 1 | ||
b=2 | ||
| 4 |
| 1 | 1 | |||
wzór szukanej funkcji: y=− | x+2 | |||
| 2 | 4 |
| 1 | ||
a=− | ||
| 9 |
| 1 | ||
wzór szukanej funkcji: f(x)=− | (x−7)2+6 | |
| 9 |
| −b−√Δ | −b+√Δ | |||
x1= | =−3 x2= | =4 | ||
| 2a | 2a |
 Wszystko przejrzyście wyjaśnione, nawet nie zdajecie sobie sprawy jak bardzo mi
pomogliście. Za to dużo zdrówka wam życzę i niech szczęście wam dopisuje. Nie wiedziałem że są
jeszcze tacy dobrzy ludzie na tym świecie. Pozdrawiam
Wszystko przejrzyście wyjaśnione, nawet nie zdajecie sobie sprawy jak bardzo mi
pomogliście. Za to dużo zdrówka wam życzę i niech szczęście wam dopisuje. Nie wiedziałem że są
jeszcze tacy dobrzy ludzie na tym świecie. Pozdrawiam
