Wyznacz zbiór wartości f(x)=x^4-4x^2+3 Madzik: Wyznacz zbiór wartości f(x)=x⁴−4x²+3 x²=t t≥0 f(x)=t²−4t+3 i co dalej, jak wyznaczyc zbiór?

Madzik: Pomoże ktoś?

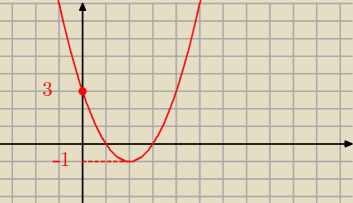
Nienor: ZbWf(x)=[−1,+∞]

PuRXUTM: f(x)=x⁴−4x²+3 x²=t f(t)=t²−4t+3=(t−1)(t−3) narysuj sobie wykres funkcji f(t) widać jasno że najmniejszą wartość f(t) przyjmuje dla t=2 więc podstawiamy za t=2 czyli x²=2 (podstawiamy do wzoru f(x)=x⁴−4x²+3 ) y=2²−4*2+3=−1 to jest najmniejsza wartość możesz sobie po kolei podstawiać kolejne x do wzoru f(x)=x⁴−4x²+3 i zobaczysz że ciągle wartość będzie rosła aż do +∞ Czyli Zw=<−1;+∞)

pigor: ..., np. tak : f(x)=x⁴−4x²+3=x⁴−4x²+4−1= (x²−2)²−1, stąd y ≥−1 ⇔ y∊[−1;+∞) . ...