jak to rozwiącać Andrzej: Równanie x⁸−x⁵+x²−x+1=0. a)ma dokładnie jeden pierwiastek rzeczywisty b)ma dokładnie dwa różne pierwiastki rzeczywiste c)nie ma pierwiastków rzeczywistych d)żadna z powyższych odpowiedzi

Andrzej: proszę o pomoc

Andrzej: ?

Andrzej: nie wiem jak to rozwiązać

Andrzej: ?

Nienor: Wyciągnij wniosek z: −jeżeli liczba całkowita jest pierwiastkiem wielomianu całkowitego o niezerowym wyrazie wolnym, to jest ona dzielnikiem wyrazu wolnego −jeżeli ułamek nieskracalny jest pierwiastkiem wielomianu całkowitego, to jest dzielnikiem wyrazu wolnego oraz jest dzielnikiem współczynnika wiodącego

Andrzej: to znaczy chyba ze to równanie nie pierwastków mam racje czy nie

Andrzej: ?

Andrzej: jak to zrobic

Andrzej: ?

Mila: Nie ma. Jednak nie mam w tej chwili rozsądnego pomysłu, to LO, czy studia?

Andrzej: lo

Andrzej: milu mam pytanie czy pomoglabyś mi rozwiącać kilka zadaniań teraz?

Mila: Wpisz zadania.

Nienor: Ach, racja, to mają być pierwiastki rzeczywiste, no to faktycznie robi się problem. Można powiedzieć, że nie ma pierwiastków wymiernych, jak na razie.

Andrzej: 1.Ciąg (an) jest rosnący, zatem ciąg (bn) o wyrazie ogólnym bn=n√⋅an jest rosnący bn=(an)4 jest rosnący bn=(an)3 jest rosnący żadna z powyższych odpowiedzi wydaje mi sie ze odpowiedzi a,b,c bedą poprawne ale do konca nie jestem oewny 2.Niech Sn=(2−3)+(22−32)+...+(2n−3n), gdzie n∈N. Wynika stąd, że Sn=2ⁿ+1−3ⁿ+1 Sn=2ⁿ+1−3ⁿ+1+1/2 Sn=4ⁿ−9 Sn=(n2)−(n3)− wzór newtona tu i tu 3.Rozważmy stożek o tworzącej długości 3 cm i wysokości długości 3√ cm. Niech P oznacza pole największego przekroju, uzyskanego przez przecięcie tego stożka płaszczyzną prostopadłą do płaszczyzny podstawy stożka. Wówczas P≤4,5 cm2 P jest równe polu przekroju osiowego przekrój o polu P jest trójkątem równobocznym żadna z powyższych odpowiedzi 4.Kąty trójkąta mają miary α,β,γ przy czym sinα/3=sinβ/4=sinγ/5. Wynika stąd, że długości boków tego trójkąta są równe 3, 4, 5 długości boków tego trójkąta są liczbami naturalnymi trójkąt ten jest trójkątem prostokątnym żadna z powyższych odpowiedzi nie jest prawdziwa 5.Istnieje taka liczba x, że: sinx=0,4 i cosx=0,8 sinx=2/3 i tgx=1/3 sinx+cosx=1 żadna z powyższych odpowiedzi

Andrzej: z góry dziekuję

Mila: 5) a) sinx=0,4⇔sin²x+cos²x=1 0,16+cos²x=1⇔cos²x=1−0,16 cosx=√0,84≠0,8 lub cosx=−√0,84≠0,8 Odp. Nie

	2
b)sinx=
	3

4		4
	+cos2x=1⇔cos2x=1−
9		9

	√5
cosx=
	3

	2		√5		1
tgx=		:		≠
	3		3		3

odp. nie c) sinx +cosx=1 ma rozwiązanie x=2kπ lub x=π/2+2kπ Tak W pozostałych muszę ustalić zapisy, bo nie wiem,czy dobrze interpretuję. 1.Ciąg (an) jest rosnący, zatem ciąg (b_n) o wyrazie ogólnym b_n=n√a_n jest rosnący b_n=(a_n)⁴ jest rosnący b_n=(a_n)³ jest rosnący żadna z powyższych odpowiedzi tak ma być? Za godzinę będę miała czas. Tymczasem rozwiąż równanie sinx+cosx=1 (wynik, podałam)

Andrzej: Milu bardzo bym cie prosił o rozwiązanie tych zadan tak przed godziną 23.00.

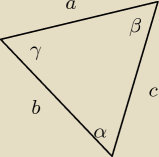
Nienor: 4. Odwrócone tw. sinusów. Tw. sinusów wygląda tak:

a		b		c
	=		=		=2R
sinα		sinβ		sinγ

I w zasadzie wszystki odpowiedzi są poprawne. 3. Pierwiastek z czego

Adam: nienor pod pierwiastkiem jest 3 a nie przed znakiem pierwiastka

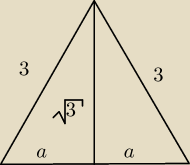
Nienor: Największe pole ma ten trójkąt, którego wysokością jest H stożka (raczej oczywiste). Wówczas a=√9−3=√6 (z tw. Pitagorasa).

	1
Pole jest równe P=		(√6+√6*√3=√2*3*√3=2√3≈5,1
	2

Przektój wzdłuż H stożka jest nazywany przekrojem osiowym. Trójkąt nie jest równoboczny.

teofrast: Odnośnie pierwszego zadania, wczoraj na forum rozwiązywaliśmy analogiczne: forum/204344.html. Oznaczając wielomian po lewej stronie jako W(x) badamy zmiany znaków przy współczynnikach W(−x). Okazuje się, że wszystkie są dodatnie: W(x) nie ma zatem pierwiastków ujemnych. Przedstawiając W(x) = ( x−1 ) (x⁷ + x⁶ + x⁵ + x) + 1, stwierdzamy, że : dla x ≥ 1 przyjmuje on wartości dodatnie, idem dla x =1 . Pierwiastki, jeśli są, będą zatem zlokalizowane w przedziale ( 0, 1). Teraz dysponujemy co najmniej 2 metodami : A) znaleźć postać quasi−kanoniczną ( suma dwóch kwadratów plus liczba ) B) posłużyć się moją metodą wskazaną w w/.w poscie, opisując wielomian P(x)=x⁸−x⁵+x²−x trójkątem, którego podstawa jest przedział [0, 1], a ramionami styczne wystawione w punktach krańcowych tego przedziału. Powodzenia!

teofrast: idem dla x=0 oczywiście... Pierwsza zaś konstatacja z twierdzenia Kartezjusza...

ZKS&: Dla x ∊ (−∞ ; −1] ∪ [1 ; ∞) x⁸ − x⁵ ≥ 0∧ x² − x ≥ 0 ∧ 1 > 0 otrzymaliśmy że dla takich argumentów wyrażenie to jest zawsze większe od 0 dla x ∊ (−1 ; 1) x² − x⁵ > 0 ∧ 1 − x > 0 ∧ x⁸ > 0 otrzymaliśmy że dla tych argumentów wyrażenie to jest zawsze większe od 0. Nasze równanie postaci x⁸ − x⁵ + x² − x + 1 = 0 tak więc nie ma pierwiastków rzeczywistych.

ZKS: teofrast to ma być sposób dla licealisty?

Mila: 2) Sn=(2−3)+(2²−3²)+...+(2ⁿ−3ⁿ), s₁=2+2²+2³+2⁴.....+2ⁿ c.g. a₁=2, q=2

	1−2n		1−2n
S1n=2*		=2*		=−2*(1−2n)=2n+1−2
	1−2		−1

s₂=3+3²+....+3ⁿ c.g b₁=3, q=3

	1−3n		1−3n		−3		−1
S2n=3*		=3*		=		*(1−3n)=		*(3−3n+1)
	1−3		−2		2		2

	1
Sn=2n+1−2+		*(3−3n+1)
	2

ZKS: Oczywiście dla x ∊ (−1 ; 1) x² − x⁵ ≥ 0 ∧ 1 − x > 0 ∧ x⁸ ≥ 0.

Mila: O! To miłe, mniej pisania. Nie odpowiedziałeś czy dobrze zrozumiałam treść zadania z ciągami, czy było założenie, żż=e a_n>0?

teofrast: ZKS bardzo ładne ( sprytne ) rozwiązanie ! Co do pytania odpowiadam. Na podobnej zasadzie, na jakiej wymaga się np. umiejętności posługiwania sie kongruencjami od gimnazjalistów na oficjalnej OMG, umiejętności rozwiązywania równań diofantycznych na OMG i OM, umiejętności rozwiązywania równań funkcyjnych na OM, umiejętności szacowania ( tzw. nierówności olimpijskie) itd itp. Wystarczy sobie wejść na stronę liceum Staszica w Warszawie, albo I LO w Białymstoku, aby skonstatować, że wszystko jest sprawą względną. Są tez kraje na świecie, gdzie wszystkie w/w zagadnienia są omawiane w ramach oficjalnego programu. Programy zresztą sie zmieniają jak w kalejdoskopie. Wystarcvz wziąc podręczniki z lat 40, 50, 60, 70, 90, ub. wieku, by to zobaczyć. Dziś jest, jutro nie ma, potem znów jest − trudno sie połapać w tej schizofrenii władz edukacyjnych. Chora władza generuje chorą szkołę. Ja pochodne i przyległości w szkole miałem; nie miałem za to kursów o wypędzaniu szatana...

Mila: Proste równania funkcyjne na OMG też były.

Mila: Nie mam odpowiedzi do treści w ciągach: a)b_n=√n a_n ? czy a) b_n=n√a_n ?

ZKS: Albo inny sposób.

	1		1		1
x8 − x5 +		x2 +		x2 − x + 1 +		x2 =
	4		4		2

	1		1		1
(x4 −		x)2 + (		x − 1)2 +		x2
	2		2		2

To wyrażenie będzie równe zero tylko wtedy gdy

	1		1		1
x4 =		x ∧		x = 1 ∧		x2 = 0
	2		2		2

widać że taka sytuacja nigdy nie zajdzie więc brak pierwiastków rzeczywistych.

ZKS: Mila skoro nie ma zainteresowanego to nie potrzebie to robimy bo widać że autor tylko czeka na gotowe rozwiązanie.

teofrast: Jesli f(x)↗ to √f(x)↗ ( pierwiastek zachowuje monotoniczność). g(x) = x ↗. Iloczyn dwóch funkcji rosnących i dodatnich jest funkcją rosnąca. Zatem jesli a_n = f(n) ↗ to b_n = n√a_n tez rosnie

Andrzej: W grupie liczącej 100 osób 40 zna język rosyjski, a 80 zna język angielski. Wynika stąd, że każda osoba z tej grupy zna język obcy oba języki zna co najmniej 20 osób oba języki zna nie więcej niż 40 osób żadna z powyższych odpowiedzi Czy tu wszustkie odpowiedzi sa poprawne?

Andrzej: ?

teofrast: Kres górny wyznacza liczba Rosjan jest ich 40 ; kres dolny wyznacza zasada włączania i wyłączania dla dwóch zbiorów: card( A∪B) = card (A) + card(B) − card (A∩B) , skad card (A∩B) =20

PW: Równanie x⁸−x⁵+x²−x+1=0 Jeszcze jeden sposób (zbliżony do ZKS) Wiadomo z nierówności między średnią arytmetyczną a geometryczną, że x⁸+x²≥2√x²x²=2|x⁵|, a więc x⁸−x⁵+x²−x+1≥2|x⁵|−x⁵−x+1≥|x⁵|−x+1 Widać, że dla x≤1 jest to wyrażenie dodatnie (w sposób oczywisty), a dla x>1 też jest dodatnie, bo wtedy x⁵>x.

Mila: Nie, 1) 40 osob może znać i rosyjski i angielski, 40 osób tylko angielski⇒20 osób nie zna żadnego z tych języków oba języki zna nie więcej niż 40 osób 2) 40+80=120 120−100=20 20 osób zna tylko język rosyjski 20 osób zna i rosyjski i angielski, 60 tylko angielski oba języki zna co najmniej 20 osób