Geometria na płaszczyźnie Janek: Prosta y=3/2x − 1 przecina boki AB i AC trojkata ABC odpowiednio w punktach K i L. Wiedzac, ze A=(3,7), B=(6,1) c=(9,9). oblicz pole trojkata AKL. Proszę o dokładne wytłumaczenie mi zadania, bo jestem całkiem zielony w geometrii na płaszczyźnie

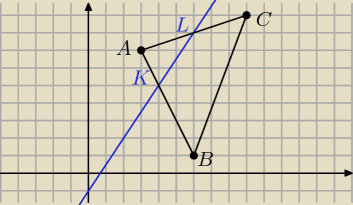
wredulus_pospolitus: krok 1 rysunek (zaznaczenie punktów A,B,C ... narysowanie boków trójkąta ... narysowanie prostej ... zaznaczenie punktów K i L − przecięcie prostej z bokami trójkąta) krok 2 wyznaczenie równań prostych k i l zawierających boki trójkata (odpowiednio) AB i AC krok 3 przyrównanie prostej podanej w zadaniu i prostej k ... w ten sposób wyznaczasz punkt przecięcia się tych prostych, czyli punkt przecięcia się prostej z bokiem AB ... czyli współrzędne punktu K krok 4 analogicznie z drugą prostą z kroku 2 krok 5 mając współrzędne wierzchołków trójkąta AKL możesz skorzystać z jednego z wielu wzorów na liczenie pola trójkąta (np. wzór Hammurabiego)

aniabb: K(4;5) L(6;8) Pole 3,5