prawdopodobieństwo luk20:

	1		1
Dane są P(A∪B)=		i P(A∩B)=		, P(A\B)=P(B\A). Oblicz P(A), P(A\B)
	2		4

asdf: Masz podpowiedź: P(A\B) = P(B\A) oznacza, ze zbiory sie zawierają w połowie i wlasnie dlatego:

	1		1
A v B =		i A ⋀ B =
	2		4

praktyczie gotowiec.

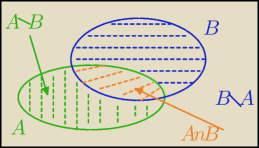Mila: P(A\B)=P(B\A) P(A∪B)=P(A)+P(B)−P(A∩B)⇔ P(A∪B)=2*P(A\B)+P(A∩B)

1		1
	=2*P(A\B)+
2		4

	1
2*P(A\B)=
	4

	1
P(A\B)=
	8

	1		1		3
P(A)=P(A\B)+P(A∩B)=		+		=
	8		4		8