 Trapezoid, to czworokąt nie mający żadnej pary boków równoległych
β= 180o−α ⇒ sinα= sinβ
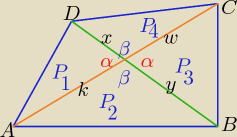
|AC|=d1, |BD|= d2 x+y=d2 , k+w= d1
P= P1+P2+P3+P4
Trapezoid, to czworokąt nie mający żadnej pary boków równoległych
β= 180o−α ⇒ sinα= sinβ
|AC|=d1, |BD|= d2 x+y=d2 , k+w= d1
P= P1+P2+P3+P4
| 1 | 1 | 1 | 1 | |||||
P1= | *k*x*sinα, P2= | *k*y*sinα, P3= | *w*y*sinα, P4= | *x*w*sinα | ||||
| 2 | 2 | 2 | 2 |
| 1 | 1 | |||
to: P= | *sinα( kx+ky+wy+xw)= | sinα[k(x+y)+w(x+y)] | ||
| 2 | 2 |
| 1 | 1 | |||
= | sinα(x+y)(k+w)= | *d1*d2*sinα | ||
| 2 | 2 |
 Prosty dowód, a nie mogłem wpaść, jeszcze raz wielkie dzięki
Prosty dowód, a nie mogłem wpaść, jeszcze raz wielkie dzięki 
