Pola figur podobnych domisimply: POLA FIGUR PODOBNYCH: 1. Punkty D, E, F dzielą bok AC trójkąta ABC na cztery odcinki równej długości. Przez te punkty poprowadzono proste równoległe do boku AB, które przecięły bok BC w punktach G, H, I. Pole trójkąta ABC jest równe 32. Oblicz pole trapezy EHIF. obrazek: http://i44.tinypic.com/2z4ihlc.png 2. Przez punkt S leżący na boku AB trójkąta ABC o polu P poprowadzono dwie proste równoległe do boków AC i BC. Te proste podzieliły trójkąt ABC na trzy części z których dwie są trójkątami o polach P1, P2. Wykaż, że pierwiastek z P = pierw. z P1 + pierw. z P2.

irena_1: 1.

	1
Trójkąt EHC jest podobny do trójkąta ABC. Ponieważ |EC|=		|AC|, więc skala tego
	2

	1
podobieństwa jest równa		.
	2

	1
Stosunek pól tych trójkątów jest więc równy s2=
	4

	1
PEHC=		PABC
	4

	1
Trójkąt FIC jest podobny do trójkąta ABC. |FC|=		|AC|, więc
	4

	1
PFIC=		PABC
	16

Stąd pole trapezu EHIF:

	1		1		3		3
PEHIF=		PABC−		PABC=		PABC=		*32=6
	4		16		16		16

Janek191: z.1 P_{Δ ABC} = 32 Trójkąty: Δ FIC i Δ ABC są podobne ( cecha podobieństwa KKK ) w skali

	I FC I		1
k =		=
	I AC I		4

zatem

PΔFIC		1		1
	= k2 = (		)2 =
PABC		4		16

więc

	1
PΔFIC =		*32 = 2
	16

−−−−−−−−−−−−−−−−−−−−−− Trójkąty: Δ EHC i Δ ABC są podobne ( cecha podobieństwa KKK ) w skali

	I EC I		1
k1 =		=
	I AC I		2

więc

PΔ EHC		1		1
	= k12 = (		)2 =
PΔ ABC		2		4

czyli

	1
PΔ EHC =		* 32 = 8
	4

−−−−−−−−−−−−−−−−−−−−−−− Pole trapezu EHIF P = P_{Δ EHC} − P_{Δ FIC} = 8 − 2 = 6 ===============================

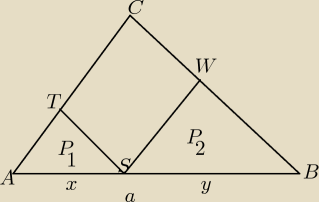irena_1: 2. Trójkąty AST i SBW są podobne do trójkąta ABC. Skale tych podobieństw:

	x		y
s1=		i s2=
	a		a

Stąd:

P1		x2		P2		y2
	=		i		=
P		a2		P		a2

√P1		x		√P2		y
	=		i		=
√P		a		√P		a

√P1+√P2		x+y		a
	=		=		=1
√P		a		a

√P=√P₁+√P₂