prawodpodobieństwo - model klasyczny luk20: Prawdopodobieństwo: W pudełku jest 6 śrubek dobrych i 2 złe. Opisać przestrzeń zdarzeń elementarnych i obliczyć prawdopodobieństwo, że wśród 4 wybranych śrubek są 3 dobre i 1 zła. Zauważyłem, że mam problem z Ω... Czy ustalając Ω podporządkowuję ją tak jakby pod moje zdarzenie? A − obl. p−stwo, że wśród 4 wybranych śrubek są 3 dobre i 1 zła, czyli czyli tak jakby lAl=6*5*4*2=240 a moja Ω={(a_i,a_j); i∊{1,2,3,4},j∊{1,2}} <− czy muszę tutaj podać jeszcze, że i≠j

	2
i lΩl=6*5*4*3=360 zatem P(A)=
	3

luk20: Wydaje mi się, że powyższa metoda nie jest jednak do końca trafna... Ale pewności też nie mam... Gdybym zrobił na kombinacje:

	6 3	2 1		8 4		4
A=			=40 Ω=		=70 i wtedy P(A)=
						7

luk20: Pomoże ktoś

Mila: II sposób prawidłowy W I błędna |Ω| i |A|. Jeżeli uwzględniłeś kolejność, to wadliwa śrubka może być wylosowana np. za pierwszym losowaniem. Popraw I sposób.

Mila: Do I sposobu narysuj sobie drzewko, to Ci duzo wyjaśni.

luk20: Ok, dzięki

Mila:

natttt: mila pomóż prosze

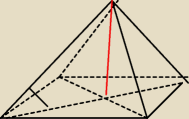
natttt: oblicz pole powierzchni całkowitej narysowanego ostrosłupa prawidłowego ta czerwona wysokość wynosi 4 ,a ten kąt 45 stopni

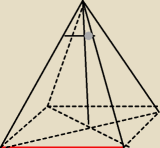
natttt: oblicz pole powierzchni całkowitej tego ostrosłupa prawidłowego ta czerwona krawędz ma 8 , a tenzaznaczony kąt ma 30 stopni

natttt: mila pomóż prosze

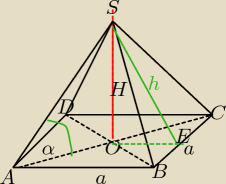
Mila: α=45⁰ H=4 ΔAOS − prostokątny równoramienny ( katy ostre po 45⁰) AO=4 AC=8 a²+a²=8² 2a²=64 a²=32=P_ABCD a=√32⇔a=4√2 OE=2√2 W ΔSOE: h²=OE²+H² h²=(2√2)²+4² h²=8+16 h=√24⇔h=2√6

	1
PΔBCS=		*4√2*2√6=4√12=4*2√3=8√3
	2

P_C=32+4*8√3 P_c=32+(32√3)j²

Mila: Natt Zakładaj nowy wątek. I dlaczego tak późno? Resztę jutro.

natttt: ale prosze to mam na jutro rano mieć

natttt: mila pomożesz te zadania z tymi kątami

Mila: Jedno masz rozwiązane, drugie rozwiążę, a na drugi raz zakładaj nowe wątki, bo do starych nie zawsze się zagląda.

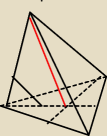
natttt: oblicz pola powierzchni całkowitej narysowanych ostrosłupów prawidłowych wysokośc tego ostrosłupa wynosi 4 pierwiastek z 3,a zaznaczony kąt ma miare 60 stopni

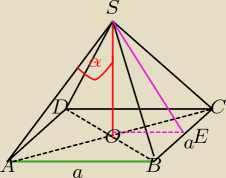
Mila: α− to kąt między krawędzią boczną, a wysokością ostrosłupa?

Mila: Napisz wyjaśnienie do postu z 19:46.

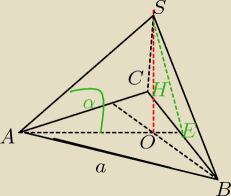
Mila: ∡SAO=α=60⁰ H=4√3 ΔSOA jest połową Δ równobocznego o boku b, SO jest wysokością tego Δ

	b√3		H
H=		⇔ ( albo sin60=		⇔AS=8)
	2		AS

b√3
	=4√3
2

b=8 |AO|=4⇔AE=4+2=6 i to jest wysokość Δ ABC

	a√3		a√3
h=		⇔		=6
	2		2

a√3=12 /*√3 3a=12√3

	(4√3)2*√3		16*3√3
a=4√3⇔PΔABC=		=		dokończ
	4		4

W Δ SOE: SE²=(4√3)²+2² |SE|²=48+4=52 |SE|=√52=2√13

	1
Pc=PΔABC+3*		a*|SE| dokończ.
	2