geometria analityczna, wektory oyyt1: Dane są wektory AC=[12,3], BC=[9,9] oraz punkt A(−5,3]. Wyznacz równania prostych, w których są zawarte wysokości trójkąta ABC....

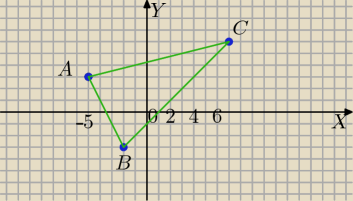
Mila: A=(−5,3) AC^→=[12,3]⇔A=(−5,3)→T[12,3]→C=(−5+12,3+3)=(7,6) BC^→=[9,9] CB^→=[−9,−9] C=(7,6)→T[−9,−9]→B=(7−9,6−9)=(−2,−3) Jakie równania piszecie? Kierunkowe, ogólne? Dokończysz?

graup33: w sumie to nieistoten jakie rownanie a co oznacza T?

graup33: okej juz wiem o co chodzi z T, ale tutaj mam w tym rozwiazaniu wierzchołki podane, a jak teraz napisac równanie prostej?

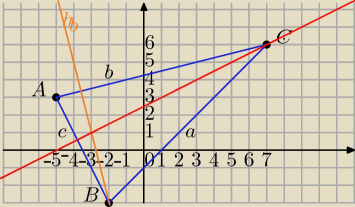
Mila: Wysokości są prostopadłe do boków A=(−5,3),C=(7,6) Prosta AC: y=ax+b⇔ 3=−5a+b 6=7a+b odejmuję stronami

	1
−3=−12a⇔a=
	4

	1
y=		x+b
	4

Wysokość opuszczona z punktu B na bok AC: h_b : y=−4x+b i B=(−2,−3)∊h_b −3=−4*(−2)+b⇔−3=8+b⇔b=−11 h_b: y=−4x−11 Prosta AB: y=ax+b 3=−5a+b −3=−2a+b odejmuję stronami 6=−3a ,a=−2 Wysokość opuszczona z punktu C na bok AB:

	1
hc : y=		x+b i C=(7,6)∊hc
	2

	1
6=		*7+b⇔b=2,5
	2

	1
hc: y=		x+2,5
	2

Trzecią prosta zawierającą wysokośc h sam napisz

Eta: Można tak: → AC=[12,3] to wektor prostopadły do prostej AC zatem h_b : 12x+3y+C=0 i B(−2,−3) € h_b ⇒ 12*(−2)+3*(−3)+C=0 ⇒ C=33 h_b: 12x+3y+33=0 −− postać ogólna ⇒ h_b: y= −4x −11 −− postać kierunkowa