Trapez równoramienny Ona_18: Podstawy trapezu równoramiennego mają długość 10cm i 6cm, a jego obwód wynosi 36 cm. Oblicz odległość punktu przecięcia jego przekątnych od dłuższej podstawy.

AROB: Pomagam

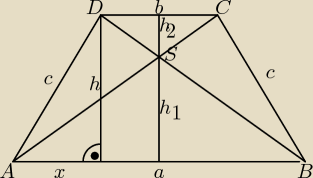
AROB: Dane: a=10 cm h₁=? b=6 cm ob = 36 cm ob = a + b + 2c 10 + 6 + 2c = 36 ⇒ c= 6 cm

	a−b		10 − 6
x=		=		= 2[cm]
	2		2

Obliczamy h z tw. Pitagorasa: h² + x² = c² h² + 4 = 100 ⇒ h² = 96 ⇒ h = √96 = =4√6 ΔABS ∼ ΔDSC ( bo równe kąty wierzchołkowe i naprzemianległe). Stąd prawdziwa jest proporcja:

	a		b
		=
	h1		h2

	10		6
		=
	h1		h−h1

	10		6
		=
	h1		4√6 − h1

6h₁ = 10(4√6 − h₁) 6h₁ = 40√6 − 10h₁ 16h₁ = 40√6 /:16

	40√6		5√6
h1 =		=		cm
	16		2