twierdzenia sinusów i cosinusów Hajtowy: Oblicz cosinus kąta ostrego pomiędzy środkowymi trójkąta prostokątnego równoramiennego, poprowadzonymi z wierzchołków trójkątów ostrych Wiem, że takie zadanie już było ale poszukuję pełnego rozwiązania i dokładnego wyjaśnienia co się skąd wzięło Proszę o skorzystanie z twierdzenia sinusów i cosinusów Z góry dziękuję

Hajtowy: I rysunek bym też prosił

Hajtowy: Pomoże ktoś ?

Hajtowy: EJ

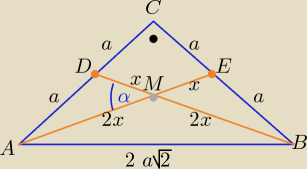
Eta: Środkowe trójkąta dzielą się w stosunku 2:1 licząc od wierzchołka |AE|=3x , |AM|=2x, |DM|=x , x>0 Z tw. Pitagorasa w trójkącie AEC

	√5a		2√5a
|AE|2= 4a2+a2 ⇒ |AE|= 3x= √5a ⇒ x=		, 2x
	3		3

	5a2
x2=
	9

z twierdzenia kosinusów w trójkącie AMD

	x2+4x2−a2		5x2−a2		16a2		9		4
cosα=		=		=		*		=
	2*x*2x		4x2		9		20a2		5

Eta: "Chłopaki nie płaczą"

Hajtowy: Przy matematyce każdy potrafi płakać Dziękuję bardzo

Eta:

Hajtowy: A mam pytanie jeszcze cosα ską się wziął licznik i mianownik? Bo nie ogarniam... Za szybko

Hajtowy: Hejo... pomoże ktoś? :'(

Hajtowy:

	x2+4x2−a2		5x2−a2		16a2		9		4
cosα=		=		=		*		=
	2x*2x		4x2		9		20a2		5

	x2+4x2−a2
Skąd się wzięło: cosα=
	2x*2x

Eta: Z tw. kosinusów:

	x2+4x2−a2
a2= x2+4x2−2*x*2x*cosα ⇒ cosα=
	2x*2x

Hajtowy: A to na dole 2a√2 to do czego? I skąd się wzięło

Eta: Akurat w tym zadaniu jest to zbędne ! d= 2a√2... dł.przekątnej kwadratu o boku "2a"

Hajtowy: Mhm. Jeszcze jedno pytanko.

	5x2−a2		16a2
Czemu po		to się równa		*{9}{20a2} skąd to ?
	4x2		9

Eta:

	5a2
No po podstawieniu: za x2=
	9

Eta: x² miało być

Hajtowy: Oke. Rozumiem

Eta: