prośba, matura rozszerzona at: cześć, jestem w klasie maturalnej LO o profilu mat−inf. Chciałabym zdawać rozszerzona maturę z matematyki. Interesuje mnie tez przedmiot, jednak nie jestem wybitna:(... nie mam funduszy na to, żeby brać korepetycje, dlatego zwracam się z prośbą o pomoc. Czy znajdzie się ktoś, kto od czasu do czasu, nie mówię, że codziennie będzie chciał zajrzeć do tego wątku i albo wsadzić jakieś zadanie typowe dla matury rozszerzonej albo mi je sprawdzić? Często bywam tu i pomagam innym, ale nie wiem na jakim poziomie są dane zadania. Ze swojej strony obiecuję codziennie i wytrwale pracować, bo bardzo mi zależy...

AS: Masz jakieś wątpliwości? A to nieładnie.

at: cieszę się, że już znalazł się ktoś, kto zechciał odpowiedzieć. Będę tu wchodzić mniej więcej co godzinkę, bo idę robić zadania z jakichś arkuszy matematycznych. Jednak już teraz wrzucę zadanie, którego nie umiem zrobić i liczę na wskazówki. R−9. zad4. Na prostej l: x+y−6=0 wyznacz taki punkt C, aby długość łamanej ACB, gdzie A(1,3), b(2,2) była najmniejsza. Uzasadnij rozumowanie. Myślałam początkowo, że długość łamanej będzie najmniejsza, jeśli stworzymy parabole, która będzie miała wierzchołek o współrzędnych C, bo było coś takiego przy funkcji kwadratowej, ale nie umiem tego rozumowania logicznie uzasadnić... potem mi przyszło do głowy, że tu musi być pewne ustawienie kąta, tak, żeby ta długość była najmniejsza, tylko nie wiem jak się za to zabrać. Dodam, że odp brzmi: c(2,5 ; 3,5)

kaz: myślę że długość łamanej będzie najkrótsza wtedy,gdy punkt na prostej będzie leżał na środku odcinka,który wyznaczą proste prostopadłe do danej prostej przechodzące przez punkty A i B

Miś: Dobrze myślisz at, a kaz się myli. Podpowiedź jest z fizyki. Światło zawsze wybiera najkrótszą drogę. Dlatego kąt padania jest równy kątowi odbicia: α=β. Punkt C jest punktem przecięcia prostej l i prostej

	1
y =		(x − 4) + 4
	3

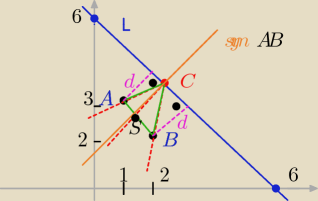
Eta: Spróbuję Ci pomóc w tym zadaniu Zacznijmy od umieszczenia punktów i prostej w układzie współrzędnych to nam uprości rozwiazanie zadania zatem z rysunku widać ,że odległości "d" są równe: sprawdźmy czy tak jest: l: x +y −6=0 A( 1,3)

	I 1*1 +3*1 −6I		2
więc d =		=		= √2
	√2		√2

dla punktu B( 2,2)

	I1*2 +2*3 − 6I		2
d =		=		= √2
	√2		√2

czyli tak jest ,,, odległości punktów A i B od prostej "l" są równe więc łamana ACB ma minimalną długość , jeżeli punkt C należy do symetralnej AB zawierającej jednocześnie punkt C ( tak jak podpowiedział [PMiś]] .. "kąt padania = katowi odbicia" wystarczy więc napisać równanie symetralnej AB wyznaczamy współrzedne punktu S( x_S, y_S)

	xA +xB		yA +yB
xS =		.... i yS=
	2		2

współczynnik kierunkowy symAB jest a = 1 bo współczynnik kierunkowy prostej l : a= −1 otrzymasz S( (³₂, ⁵₂) sym.AB: y − y_S = 1( x − x_S) wyznacz równanie tej symetralnej i rozwiązując układ równań a prostą "l" otrzymasz współrzedne punktu C Odp: rzeczywiście taka jak podałaś: C( ⁵₂, ⁷₂) by łamana ACB miała najmniejszą długość Pozdrawiam , życzę powodzenia

AS: Mam wątpliwości czy droga jaką przyjąłem jest poprawna. Zamiast rozpatrywać drogę s = AC + BC przyjmuję s = AC² + BC² A(1,3) , B(2,2) , C (x,6−x) AC² = (x − 1)² + (6 − x −3)² = x² − 2*x + 1 + 9 − 6*x + x² = 2*x² − 8*x + 10 BC² = (x − 2)² + (6 − x − 2)² = x² − 4*x + 4 + 16 − 8*x + x² = 2*x² − 12*x + 20 s = AC² + BC² = 4*x² − 20*x + 30 sw = −b/(2*a) = 20/8 = 5/2 yw = 6 − xw = 6 − 5/2 = 7/2 Odp. C(5/2,7/2)

AS: Można też przyjąć taką wersję Suma s = AC + BC będzie najmniejsza gdy AC = BC Wtedy AC = √(x − 1)² + (3 − x)² BC = √(x − 2)² + (4 − x)² Wykorzystując poprzednie obliczenia mamy 2*x² − 8*x + 10 = 2*x² − 12*x = 20 4*x = 10

	5
x =
	2

	7
y = 6 − 5/2 =
	2

at: R−7 zad4. W trójkącie równoramiennym ABC (IACI=IBCI=a) poprowadzono wysokości CK i AM. Wiedząc że IABI²=ICKI*IAMI wyznacz cosinus kąta przy podstawie trójkąta. Moje rozwiązanie: z tw. Pit: 0,25IABI²+ICKI²=a² a=√ 0,25IABI²+ICKI² { ICMI²+ IAMI²=a² { IBMI²+ IAMI²=IABI² +_________________ a² + 2IAMI²=a²+IABI² (bo CM+AM=a) IAMI=1/√2 IABI z danych: IABI²=ICKI*IAMI IABI²=ICKI*1/√2 IABI ICKI=√2IABI ICKI²=2IABI²

	0,5IABI
cosα=		=1 3
	√ 0,25IABI2+2IABI2

a odpowiedź ma być: nie ¹ ₃ tylko √2−1 kto mi wytłumaczy gdzie robię błąd?

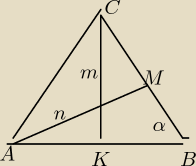
AS: Dane AB² = CK*AM Szukane cos(α) Rozwiązanie

	1
CK =		*AB*tg(α) AM = AB*sin(α) wstawiam do związku podanego
	2

	1
AB2 =		*AB*tg(α)*AB*sin(α) | :AB2
	2

	sin(α)
2 = tg(α)*sin(α) ⇒ 2 =		*sin(α)
	cos(α)

2*cos(α) = sin²(α) 2*cos(α) = 1 − cos²(α) cos⁽α) + 2*cos(α) − 1 = 0 po wyliczeniu deltą I cos(α) = −1 − √2 II cos(α) = −1 + √2

AS: CM² + BM² nie równa się a²

at: dziękuję za rozwiązanie. Swoja drogą zrobiłam głupkowaty błąd i nie mogłam go znaleźć.