Równoległobok bełehehłe: Przekątne równoległoboku o polo 16 √2 przecinają się pod kątem którego sinus wynosi 2√2/2. Jedna z przekątnych jest 3 razy dłuższa. Oblicz obwód równoległoboku.

Kejt:

	2√2
sinx=		?
	2

to niemożliwe, bo:

	2√2
sinx=		=√2≈1,41
	2

a Z_w sinx∊<−1;1>

bełehehłe: 2√2/3 Przepraszam za błąd.

Kejt:

bełehehłe: Mogę liczyć na pomoc?

Kejt: tak, liczę.

bełehehłe: Ok, dzięki.

bełehehłe: I jak?

Kejt: skanuję masz może odpowiedzi?

bełehehłe: Oczywiście. Obwód= 8(√2 + √3) cm

Kejt: kurde.. chyba się walnęłam przy liczeniu drugiego boku, ale sposób masz więc sobie sam dokończysz

bełehehłe: No myśle, że na spokojnie. Nie jestem aż tak zły z matmy

bełehehłe: Ale mogłabyś wrzucić to co zrobiłaś

Kejt: łee. tak to żadna sztuka błąd znaleźć sekundę.. skaner mnie nie kocha..

bełehehłe: Dobrze, czekam spokojnie

Kejt: w końcu.. to chyba cud: http://speedy.sh/kmJ33/Scan-130521-0003.jpg

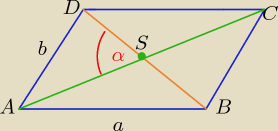
Eta: |AC|=f , |BD|= e Z treści zadania : f=3e

	1		3		2√2
P=		*e*f*sinα=		e2*		= 16√2 ⇒ e=4 , to [c]f=12]]
	2		2		3

	8		1
sin2α=		to cosα=
	9		3

z twierdzenia cosinusów w trójkącie ASD:

	1
b2= 22+62−2*2*6*		⇒ b2= 32 ⇒ b=4√2
	3

w każdym równoległoboku : e²+f²= 2a²+2b² ⇒ a²= .......... ⇒ a=4√3 Obwód L= 2(a+b)=........... = 8(√3+√2) [j]