geometria Ania: GEOMETRIA, TO DLA MNIE CZARNA MAGIA..... BŁAGAM O POMOC .. Na okręgu opisano trapez prostokątny. Odległości środka okręgu od końców dłuższej podstawy wynoszą 8₍2} cm i 17 cm. Oblicz pole trapezu...

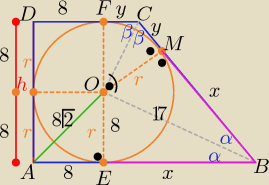
Eta: |AO|=8√2 ⇒ r=8 , h=2r=16 z tw, Pitagorasa w trójkącie BOE x²=17²−8² ⇒ x= 15 a=|AB|=8+x= 23

	64
w trójkącie prostokątnym BOC r2=x*y ⇒ y=
	15

b=|DC|= 8+y= ..........

	a+b
P(tr)=		*h= ........... dokończ
	2

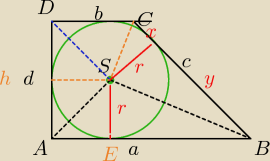Mila: |SA|=8√2 |SB|=17 a+b=c+d, d=2r ΔCSD− Δ prostokątny równoramienny d²=(8√2)²+(8√2)²=64*2+64*2=256 h=d=16 r=8 AE=8, SB²=r²+EB² 17²=8²+EB² 289−64=EB² EB²=225⇔EB=15 y=EB=15 − punkty styczności okręgu są równo odległe od wierzchołka kata ΔCSB− Δ prostokatny. r=√x*y 8=√x*15 64=x*15

	64
x=
	15

	4
c=15+4
	15

	4		4		529
d+c=16+19		=35		=
	15		15		15

	1
Ptrapezu=		(d+c)*h
	2

	1		529
Ptrapezu=		*		*16 oblicz
	2		15

Eta: Ejj Mila

Mila: Witaj, Eto pisałam dość długo, doglądając kuchennych smakołyków.