zadanie z podobienstwa trojkatów
karolina: W trójkącie prostokątnym ABC przyprostokątne AB i AC mają dlugosc 12 cm i 16 cm. AD jest
wysokością w tym trójkącie. Oblicz stosunek pól trójkątów:
a) ABD i ABC
b) ADC i ABC
c) ABD i ADC
wyliczyłam z pitagorasa długosc przeciwprostokątnej i nie wiem, co mam dalej zrobic w tym
zadaniu

17 wrz 22:24
Kalumniatoris:
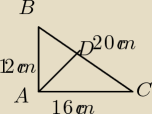
Chodzi o taki trójkąt?
17 wrz 22:30
karolina: tak

17 wrz 22:32
AROB: Będziesz liczył, Kalumniatoris ? Bo nie wiem, czy mam pisać.
17 wrz 22:34
Kalumniatoris: czyli |AD| = 9.6cm
12*16/2=96 | 96/20*2=9.6
Nie jestem pewien czy to jest potrzebne ale podam.
Teraz trzeba obliczyć w jakim stosunku punkt D dzieli bok BC
17 wrz 22:36
Kalumniatoris: AROB pisz śmiało
17 wrz 22:36
AROB: Pomagam.
17 wrz 22:38
karolina: w jakim stosunku punkt D dzieli bok BC − to mogę obliczyc,obliczajac pitagorasem DC, chyba.
17 wrz 22:46
Kalumniatoris: karolina: masz rację.
17 wrz 22:50
AROB:
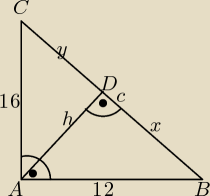
c już wyliczyłaś, c=20 cm
| | 1 | |
PABC = |
| *12*16 = 96 cm2 |
| | 2 | |
| | x | | h | |
ΔABC∼ΔABD, stąd prawdziwa jest proporcja: |
| = |
| |
| | 12 | | c | |
| | 1 | | 1 | |
Z tej proporcji x= 712, y= c−x= 20 − 7 |
| = 12 |
| |
| | 2 | | 2 | |
Obliczam potrzebne h z ΔABD: X
2 +h
2 =12
2, stąd h=9,6 cm
| | 1 | | 1 | | 1 | |
PABD = |
| * x * h = |
| * 7 |
| *9,6 = ...36 [cm2] |
| | 2 | | 2 | | 2 | |
| | 1 | | 1 | |
PADC = |
| *h*y = |
| *9,6 * 1212 = 60 [cm2] |
| | 2 | | 2 | |
No i podstawić pola do żądanych stosunków:
17 wrz 23:03
karolina: dziękuję bardzo za pomoc

17 wrz 23:13
AROB: 
17 wrz 23:17
problem1234: skąd wzieła sięproprocja x/12=h/c, nie ogarniam, pomocy!
24 maj 19:11
Eta:
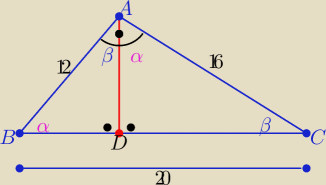
Zadanie sprzed 8 lat

|BC|=
√122+162= 20
1/ trójkąty ABD i ABC są podobne z cechy (kkk)
| | 12 | | 3 | | P(ABD | | 9 | |
w skali k= |
| = |
| to |
| = k2= |
| |
| | 20 | | 5 | | P(ABC) | | 25 | |
analogicznie
| | 16 | | 4 | | P(ADC) | | 16 | |
2/ trójkąty ADC i ABC podobne w skali k= |
| = |
| to |
| = |
| |
| | 20 | | 5 | | P(ABC) | | 25 | |
| | 12 | | 3 | | P(ABD) | | 9 | |
3) trójkąty ABD i ADC podobne w skali k= |
| = |
| to |
| = |
| |
| | 16 | | 4 | | P(ADC) | | 16 | |
24 maj 22:36

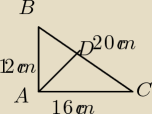 Chodzi o taki trójkąt?
Chodzi o taki trójkąt?

 c już wyliczyłaś, c=20 cm
c już wyliczyłaś, c=20 cm


 Zadanie sprzed 8 lat
Zadanie sprzed 8 lat  |BC|=√122+162= 20
1/ trójkąty ABD i ABC są podobne z cechy (kkk)
|BC|=√122+162= 20
1/ trójkąty ABD i ABC są podobne z cechy (kkk)