W trójkącie dwa boki mają długość 12 i 3, a kąt między nimi jest równy 60 stopni erytrocyt: W trójkącie dwa boki mają długość 12 i 3, a kąt między nimi jest równy 60 stopni. Oblicz: promień okręgu opisanego na trójkącie promień okręgu wpisanego w trójkąt

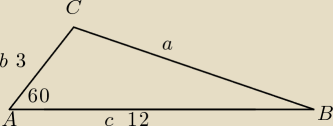
Mila: z tw. cosinusów a²=3²+12²−2*3*12 cos 60

	1
a2=9+144−2*36*
	2

a²=153−36 a²=117 a=√117=√9*13 a=3√13 Z tw sinusów:

a
	=2R
sin60)

	√3
3√13: (		)=2R
	2

	2
3√13*		=2R
	√3

	6√13
2R=		usuwam niewymierność z mianownika
	√3

	6√39
2R=
	3

R=√39− promień okręgu opisanego na tym Δ

	1
PΔ=		*3*12*sin60=9√3
	2

	1
PΔ=p*r⇔9√3=		*(3+12+3√13)*r
	2

18√3=(15+3√13)*r /:3 6√3=(5+√13)*r

	6√3
r=		Usuwamy niewymierność
	5+√13

	6√3*(5−√13)		6√3*(5−√13)
r=		=
	25−13		12

	5√3−√39
r=
	2