f kwadratowa funkkcja: W trójkąt prostokątny równoramienny o przyprostokątnych długości 6cm wpisano prostokąt tak, że jeden jego bok zawiera się w przeciwprostokątnej, a dwa pozostałe wierzchołki należą do ramion trójkąta. Wyznacz wymiary prostokąta o największym polu

Eta: Pomagam

Janek191: b = c = 6 cm a = a √2 = 6 √2 cm x −długość prostokąta y − szerokość prostokąta h − wysokość trójkąta h = 0,5 a= 3 √2 Z podobieństwa trójkątów mamy

x		h − y
	=
a		h

czyli

x		3 √2− y
	=
6 √2		3 √2

3 √2 x = 6 √2*( 3 √2 − y) ./ : 3 √2 x = 6 √2 − 2y ⇒ 2y = 6 √2 − x y = 3 √2 − 0,5 x −−−−−−−−−−−−−−−−−−−−−− Pole prostokąta P = x*y = x*( 3 √2 − 0,5 x) − 0,5 x² + 3 √2 x P(x) = − 0,5 x² + 3 √2 x a = − 0,5 < 0 − ramiona paraboli skierowane są ku dołowi − funkcja posiada największą

	− 3 √2
wartość dla x = p =		= 3 √2
	− 1

Wtedy y = 3 √2 − 0,5* 3√2 = 1,5 √2 Odp. Wymiary prostokąta o największym polu : x = 3 √2, y = 1,5 √2 =========================================================

Eta:

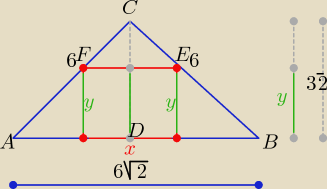
	1
|AB|= 6√2 i |CD|=		|AB|=3√2
	2

z podobieństwa trójkątów ABC i EFC:

	6√2		3√2		36−6√2
		=		⇒ y=
	x		3√2−y		6√2

pole prostokąta : P=x*y

	36−6√2x		1
P(x)= x(		)= −		x2−3√2x −−− parabola ramionami do dołu
	6√2		2

to funkcja osiąga maksimum dla odciętej wierzchołka

	−3√2
xmax=		= ........
	2*(−12)

y_max= .... dokończ.....

Eta: Przecież napisałam,że pomagam!

Janek191: Jak zacząłem , to nie było jeszcze tej informacji

Eta:

Janek191: Właśnie tego rysunku brakowało

funkkcja: Dziękuję za pomoc