Funkcje trygonometryczne
Marque: Oblicz pole trójkąta ABC i wyznacz miarę kąta ABC, mając dane |AC|=4, |AB|=2(1+√3), |∡A|=60
stopni.
Proszę o pomoc. Proszę aby rozwiązanie opierało się na funkcjach trygonometrycznych.
19 maj 15:20
Krzysiek : To moze najpierw narysuj ten trojkat jak bedzie wygladal i pooznaczaj
19 maj 15:30
Krzysiek : Jest tez wzor na pole trojkata gdy masz 2 boki i kat pomiedzy tymi bokami P=a*b*sinα
19 maj 15:33
Marque:
Kąt przy A=60 stopni
|AC|=4
|AB|=2(1+
√3)
Tylko tyle danych w zadaniu. Rysunku w zadaniu też nie było, sam go skonstruowałem.
19 maj 15:36
Marque: OK Krzysiek, wzór jest okey, ale jak mam wyznaczyć sinα? Co do czego?
19 maj 15:40
Marque: Aha już wiem, pole to będzie:
4(2+2√3)*√32
19 maj 15:42
Kaja: | | √3 | |
to jest sin600 czyli |
| |
| | 2 | |
19 maj 15:42
Marque: Okey, pole już obliczyłem, wynosi 4√3+12cm2.
Ale jak teraz policzyć miarę kąta ABC?
19 maj 15:44
Marque: Jakieś pomysły?
19 maj 16:27
ciekawski: np.
|CB|/sinα=|AC|/sin∡β
α−kąt przy A; β−przy B
19 maj 16:36
Marque: Okey ciekawski, ale nie mam ani długości CB, ani kąta przy B...
19 maj 16:41
Mila:
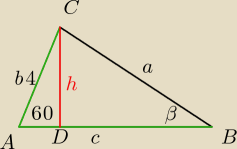
c=|AB|=2(1+
√3)
| | 1 | | √3 | |
PΔ= |
| *2(1+√3)*4*sin60=4(1+√3)* |
| ⇔ |
| | 2 | | 2 | |
P
Δ=2(
√3+3)
|AD|=2
|DB|=2+2
√3−2=2
√3
| | h | | 2√3 | |
tgβ= |
| ⇔tgβ= |
| =1 |
| | |DB| | | 2√3 | |
β=45
0
19 maj 17:08
Marque: Mila, stokrotne dzięki

!
19 maj 17:22
Mila: 
19 maj 17:33
 Kąt przy A=60 stopni
|AC|=4
|AB|=2(1+√3)
Tylko tyle danych w zadaniu. Rysunku w zadaniu też nie było, sam go skonstruowałem.
Kąt przy A=60 stopni
|AC|=4
|AB|=2(1+√3)
Tylko tyle danych w zadaniu. Rysunku w zadaniu też nie było, sam go skonstruowałem.
 c=|AB|=2(1+√3)
c=|AB|=2(1+√3)
 !
!
