Całka nieoznaczona 'me~:

	x−2
Witam. Potrzebuję wsparcia w takiej oto całce: ∫x√		. Próbowałem przez podstawienie
	4−x

i przez części ale mi nie wychodzi

'me~: odświeżam

'me~: no to jeszcze raz

'me~: i znowu

'me~: patrzę, że chyba się nie doczekam...

'me~: to dzięki za pomoc, dużo się dowiedziałem

Mila: Metodą współczynników nieoznaczonych. Przekształcamy wyrażenie:

	√x−2		√x−2)2		x(x−2)
∫x*		dx=∫x		dx=∫		dx=
	√4−x		√(x−2)(4−x)		√(x−2)(4−x)

	x2−2x
=∫		dx
	√−x2+6x−8

Rozwiązanie ma postać:

	x2−2x		A
∫		dx=(ax+b)*√−x2+6x−8+∫		dx
	√−x2+6x−8		√−x2+6x−8

Zróżniczkuj obustronnie i wyznacz wsp. a,b,A

Mila: Jeśli Ci nie wyjdzie, to jutro napiszę.

'me~: Wyszła, nie pomyślałem, żeby podprowadzić do metody współczynników nieoznaczonych. Znalazłem

	arcsinx
chyba lepszą całkę. ∫		dx próbowałem obliczyć przez części, ale wychodzi 0=0.
	x2

Chyba jest na to jakiś wzór rekurencyjny, ale nie pamiętam go...

Mila:

	arcsinx		−arcsinx		dx		−arcsinx
∫		dx=		+∫		=		+J1
	x2		x		x√1−x2		x

	1		1		1		−1
[arcsinx=u,		dx=du, dv=		dx, v=∫		dx=		]
	√1−x2		x2		x2		x

	dx
J1=∫		= przez podstawienie
	x√1−x2

	1		1		−1
[		=t, x=		, dx=		dt] dokończysz ?
	x		t		t2

'me~: pewnie tak a jak nie to napiszę

'me~: Mam jeszcze jedno zadanie z którym mam problem. Oblicz pole figury ograniczonej liniami:

⎧	x=a*cost
⎩	y=b*sint

Zrobiłem sobie założenie, że 0≤t≤2π Podstawiłem do wzoru P=₀∫^2π|a*cost*(−bcost)|dt i tu pojawia się problem czy mogę sobie opuścić normalnie wartość bezwzględną i policzyć całkę nieoznaczoną? Niby pole nie może być ujemne, ale nie jestem pewien czy tak można

Mila: PO 20, zobaczę.

'me~: ok, czekam z niecierpliwością

Mila: Ta krzywa to elipsa. x(t)=a cos(t), a>0 y(t)=a sin(t) , sin(t)≥0 dla t∊<0,π> 1) t∊<0,π> Ponieważ x(t)=a cos(t) jest w tym przedziale malejąca to pole obliczamy wg wzoru: P₁=−₀∫^π|y(t)|*x'(t) dt= −∫bsin(t)*(−asin(t)) dt=ab*₀∫^πsin²(t)dt 2) dla x∊<π,2π> funkcja x(t)=a cos(t) jest rosnąca, to pole obliczamy wg wzoru: P₂=_π∫^2π|y(t)|*x'(t) dt=∫(−bsin(t))*(−a sin(t))dt=ab*∫sin²(t) dt ( taki sam wzór jak dla P₁) P=P₁+P₂=ab* ₀∫^2πsin²(t)dt

	1
sin2(t)=		(1−cos(2t)) ( ze wzoru na cos (2x)=cos2x−sin2x)
	2

	1		1
P=		ab0∫2π(1−cos(2t)dt=		ab*[(t−0,5sin(2t)|02π=
	2		2

	1
=		ab[2π−0,5*sin4π−0+sin0]=abπ
	2

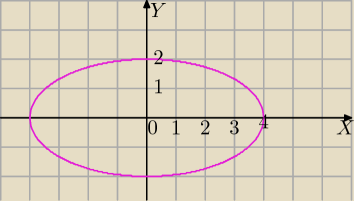
Mila: Elipsa dla a=4 i b=2 {x=4 cost, y=2 sint} x²=16 cos²t y²=4 sin²t ⇔

x2
	=cos2t
16

y2
	=sin2t dodaję stronami
4

x2		y2
	+		=1
16		4

x2		y2
	+		=1
42		22

'me~: zawsze biorę pod uwagę tylko dodatnie wartości sinusa albo cosinusa tak?

Mila: Jeśli chodzi o |sinx|=sinx dla x∊<0,π> |sinx|=−sinx dla x∊(π,2π) Nie wiem o jaki fragment Ci chodzi.

Mila: Jeśli chodzi o |sinx|=sinx dla x∊<0,π> |sinx|=−sinx dla x∊(π,2π) Nie wiem o jaki fragment Ci chodzi.

'me~: bo założyłaś, że sin(t)≥0 dla t∊<0,π> a zastanawiam się czemu musi przyjmować wartości dodatnie?

Mila: We wzorze występuje |sint|, to rozważam, kiedy mogę opuścic znak wartości ||, aby dalej liczyc. z definicji: |a|=a dla a≥0 |a|=−a dla a<0

'me~: ok, dziękuję za pomoc

Mila: Miałam kłopoty z dostępem do strony, też cos zauważyłeś?

'me~: tak, myślałem już, że Twoje wysiłki poszły na marne, ale na szczęście nie

'me~: Zrobiłem inny przykład i podszedłem do niego troszkę inaczej. Zobacz

⎧	x=a(t−sint)
⎩	y=a(1−cost	a>0 i t∊<0,2π>

Wziąłem przedział od 0 do ^π₂ gdzie sin jest dodatni wiec P=4₀∫^π₂|(a−acost)*(a−acost)|dt I jak?

Mila: Jutro. Muszę Ci wytłumaczyć wzór, albo poczytaj w podręczniku. Tu bierzesz |1−cos(t)|=1−cos(t) dla każdego t, bo |cost|≤1 Dobranoc.

'me~: ok dobranoc

Mila: Krzywa jest cykloidą. x=a(t−sint) y=a(1−cost) a>0 i t∊<0,2π> Badamy monotoniczność funkcji x(t)=a(t−sint) x'(t)=a(1−cost) a(1−cos(t))≥0 dla każdego t, zatem x(t) jest rosnąca w przedziale <0,2π>, w takim razie P=₀∫^2π|y(t)|*x'(t)dt= =₀∫^2π|a(1−cos(t)|*a(1−cos(t)dt=a²₀∫^2π(1−2cost+cos²(t))dt=

	1
=a20∫2π(1−2cos(t)+		(cos(2t)+1))dt
	2

	1		1
=[a2*(t−2sin(t)+		sin(2t)+		t)]02π=
	4		2

	1		1
a2(2π−2sin(2π)+		sin(4π)+		*2π)=a2*(2π−0+0+π)=
	4		2

=3πa² Pole cykloidy jest równe potrojonemu polu toczącego się koła o promieniu a>0.