geometria , płaszczyzny... bartekcmg: 1. Znaleźć równanie płaszczyzny zawierającej pkt (−3,1,−2) i oś 0z . ( ps. jakie współrzędne ma oś 0z?) 2.Znaleźć równanie tej płaszczyzny zawierającej pkty (4,0,−2) oraz (5,1,7), która jest równoległa do o si 0x. Z góry bardzo dziękuję za odpowiedzi

ff: oś oz : np. parametrycznie: x=0,y=0,z=t , t ∊ R ad 1: płaszczyzna zawiera oś z − więc jest prostopadła do płaszczyzny oxy − jej równanie to równanie prostej przechodzącej przez punkty (−3,1) i (0,0) na pł. oxy π₁ : y = −¹₃x π₁ : x + 3y = 0 ad 2. podobnie, płaszczyzna jest równoległa do osi 0x − więc jest prosotpadła do płaszczyzny oyz − rzutujemy punkty na pł. oyz − równanie płaszczyzny to równanie prostej przechodzącej przez: (0,−2), (1,7) na pł. yz π₂: y − 2 = 7z π₂: y − 7z = 2

ff: ech − ad2.: π₂ : z = 9y − 2

bartekcmg: nie rozumiem skąd się wzięło równanie x+3y=0

bartekcmg: bardzo proszę o wyjaśnienie

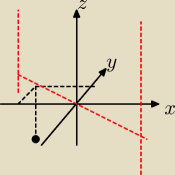
ff: płaszczyzna zawiera oś z, więc zawiera punkt (0,0,0), wystarczy, że zrzutujemy punkt (−3,1,2) na oxy: (−3,1) i równanie płaszczyzny to równanie prostej przechodzącej przez (−3,1) i (0,0) na 0xy

bartekcmg: świetnie dziękuję bardzo... a w drugim skąd dziewiątka ps.: w odpowiedziach mam: 9y−z−2=0

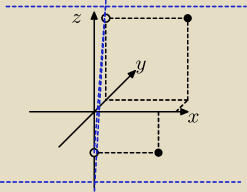
ff: równanie prostej przechodzącej przez (0,−2) (1,7) na 0yz (ew. przez (0,0,−2) i (0,1,7)) (poprawiłem się w 12:43)

bartekcmg: równanie prostej to wiem, ale skąd 9? (7+2) ale wtedy skąd ta kolejna −2

bartekcmg:

ff: wyznacz równanie prostej przechodzącjej przez punkty (0,−2) i (1,7)